

Napoleon's Triangle
Elizabeth Nelli
If equilateral triangles are constructed on the sides of any given triangle, the centers of those equilateral triangles will form an equilateral triangle. This triangle is called Napoleon’s Triangle and is attributed to Napoleon Bonaparte. When the triangle is flipped inside out, Napoleon’s Triangle shrinks, but remains equilateral. The difference in the area of the first Napoleon’s Triangle and the second equals the area of the original triangle.
While Napoleon’s name is attributed to the theorem, there is speculation as to whether or not he actually came up with the proof. The first written documentation of this proof came out 4 years after the emperor’s death and was seen in The Ladies’ Diary which was an annual periodical in London from 1704-1841. It included a range of information from phases of the moon to important dates. Each year readers submitted questions for others to solve and the answers were posted in the following year’s issue.
Below is the outer Napoleon’s triangle:
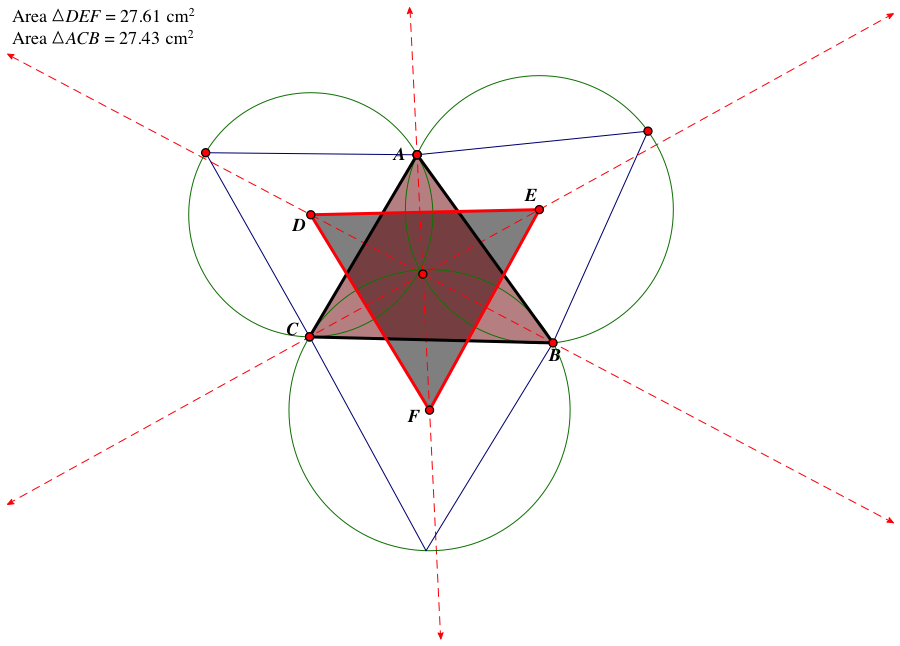
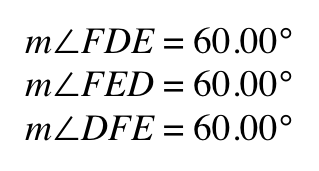
Below is the inner Napoleon's Triangle:
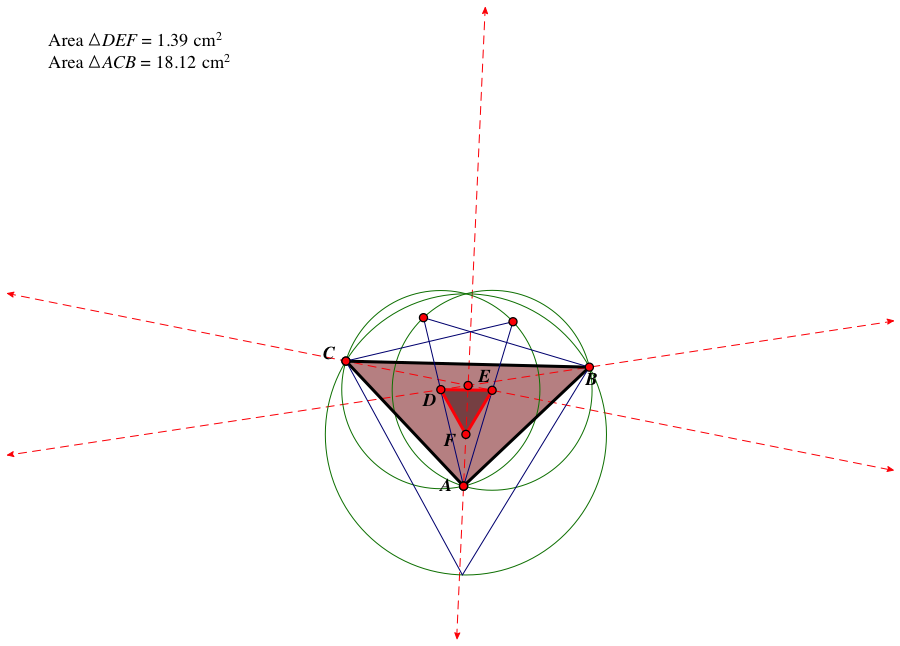
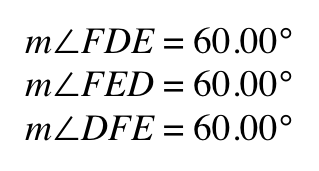
GSP shows us that the measure's of the angles of triangle DEF remain at 60 degrees for both the outer and inner Napoleon's triangles.
However, GSP is not a sound source for proving a triangle is equilateral. Below is the proof that Napoleon's Triangle is equilateral:
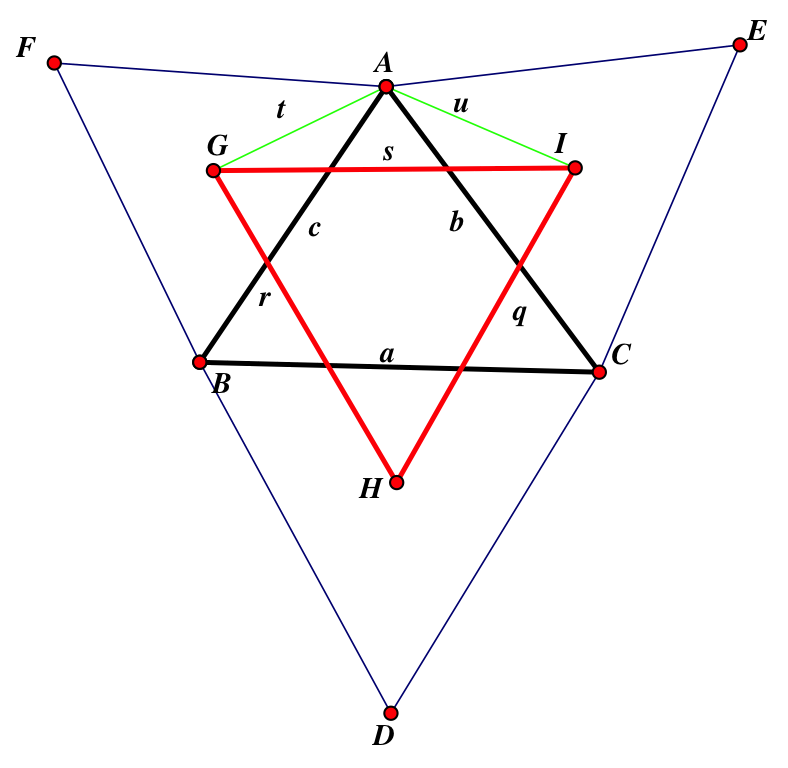
∆ABC is the original triangle.
A is the vertex and <A
a is BC and its length
b is AC and its length
c is AB and its length
G is the centroid of ∆FBA, I is the centroid of ∆ECA and H is the centroid of ∆BCD.
s is GI and its length
r is GH and its length
q is HI and its length
t is the length of AG
u is the length of AI
<IAC=<GAB=30°
Compute using Law of Cosines
s2=u2+t2-2ut•cos(A+60°) (1)
The centroid of a triangle lies along each median (put in proof from last semester), 2/3 of the distance from the vertex to the midpoint of the opposite side we get
t=(2/3) • (√3)/2•c =c/(√3)
u=(2/3) • (√3)/2• b =b/(√3)
and (1) becomes 3•s2=b2+c2-2bc•cos(A+60°) (2)
cos(60°)= ½ ; sin(60°)= (√3)/2
cos(A+60°)=cos(A)/2•(√3)/2 (3)
Substitute (3) into (2) and get:
3•s2=b2+c2-bc•cos(A)+(√3)•bc•sin(A) (4)
Apply the Law of Cosines to ∆ABC:
a2=b2+c2-2bc•cos(A) (5)
2•Area(∆ABC)=bc•sin(A) (6)
Substitute (5) and (6) into (4):
3•s2=( ½ )(a2+b2+c2)+2•(√3)•Area(∆ABC) (7)
(7) is symmetrical in a, b, and c that means the triangle connecting at the 3 centroids is equilateral
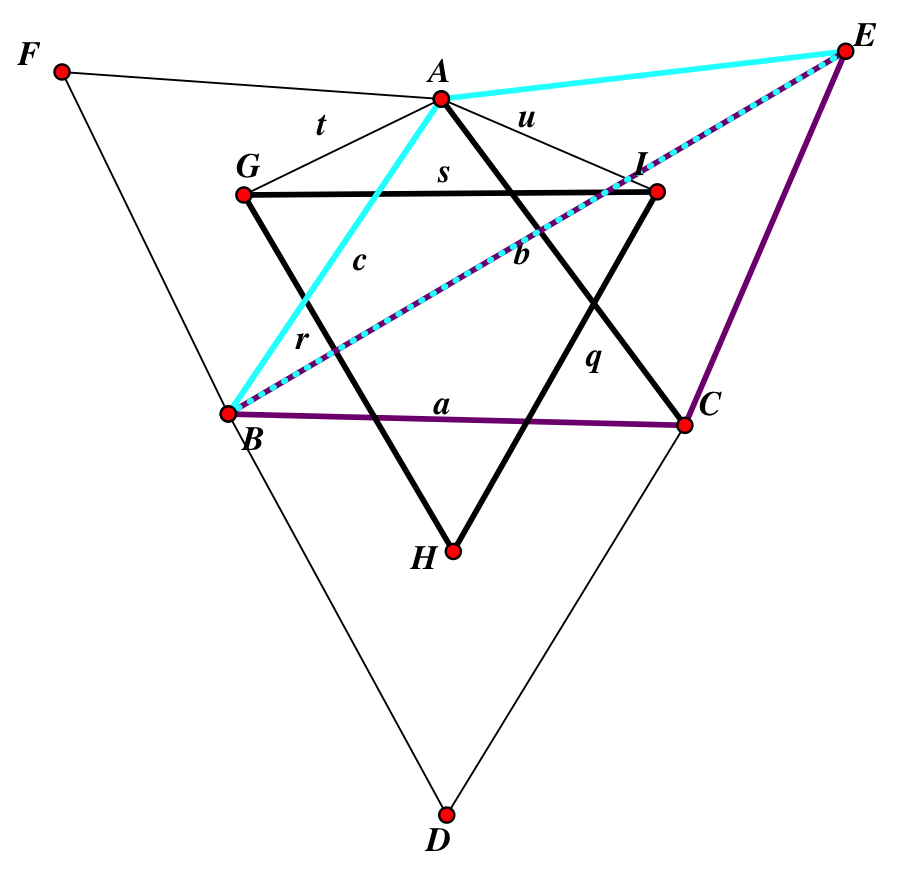
ALTERNATE WAY AFTER (2)
Apply the Law of Cosines to ∆ABE and ∆BCE to show BE in two different ways:
b2+c2-2bc•cos(A+60°)-a2+b2-2ab•cos(C+60°)
By (2), the left hand side of the equation equals 3 times GI and the right hand side of the equation equals 3 times IH (GI=IH). Using the same process but with ∆ACD and ∆ABD instead we find that IH=HG which means that IH=HG=GI. QED