Because we can only take a square root of a positive number, this is also sometimes the definition of absolute value:

With absolute value functions, a negative x-value maps to a positive y-value. We know what the graph of the absolute value of y=|x| looks like a V through the origin.

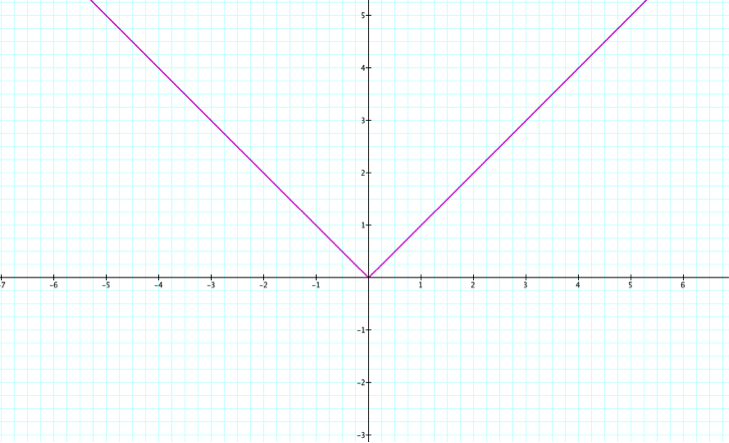
|x| is a mapping for some domain of x. If the domain is all-real numbers then
for x=0, |x|=0
for x<0, |x|=-x
for x>0, |x|=x

Now let’s take a look at another function. |y|=x

Again, we have a V through the origin, but as we can see this V is turned 90 degrees to the right. This is because a negative y-value maps to a positive x-value.

|y| is a mapping for some domain of y. If the domain is all-real numbers then
for y=0, |y|=0
for y<0, |y|=-y
for y>0, |y|=y

Back to y=|x|
We can change where the absolute value is on the graph by adding or subtracting constants. Take y=|x|+2

The graph has moved up 2 points on the y-axis.

But is we put the 2 inside of the absolute value symbol, then the graph moves along the x-axis. Careful, a positive constant value inside the absolute value symbol will move the graph to the left and a negative constant inside will move the graph to the right.

y=|x-2|

y=|x+2|

We can also change the width of the graph by multiplying by a constant. 

y=|3x+2|

y=|1/2x+2|

Or flip the graph upside down by placing a negative sign outside of the absolute value symbol.

y=-|x|

 

Relationship to the sin function
The absolute value function of any real number will remain positive. Take a look at the graph of y=sin(x)

 

We can see that there are negative y-values on the graph. But if we take the absolute value of sin(x), there will not be any negative y-values because the x-values map onto positive y-values.

 

So this gives us a little bit of insight into the absolute value function. All negative x-values map to a positive y-value when y=|x|, for all real numbers x.