

Parametric Equations of Circles
Elizabeth Nelli
We are exploring different parametric equations. For this, we will be exploring 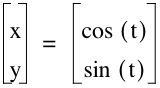
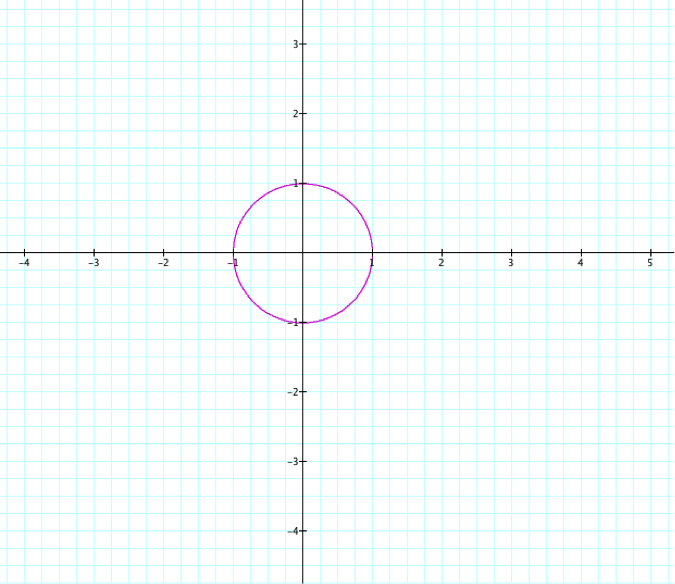
In order to do so, we must set a range for t. First, we will explore t: 0...1
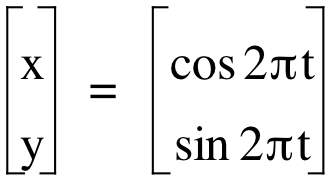
this draws a circle parametrically
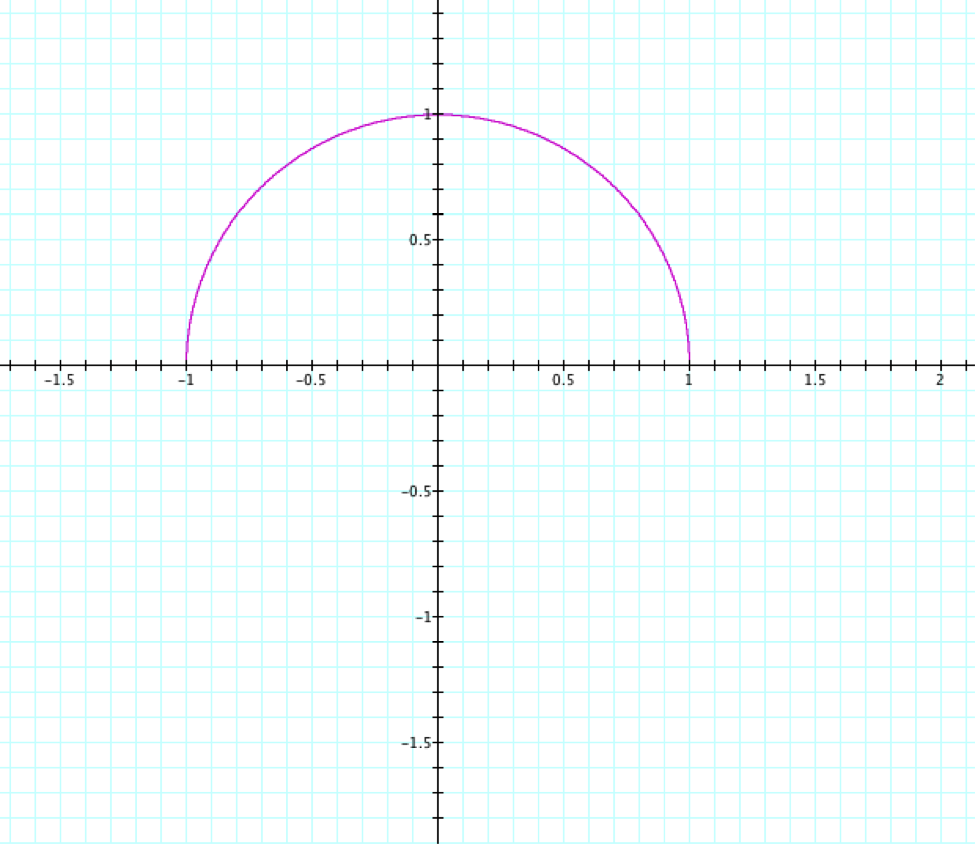
When we use the same equations, but instead use a range of t:0...0.5, we end up with a semi-circle.
t: 0....0.25
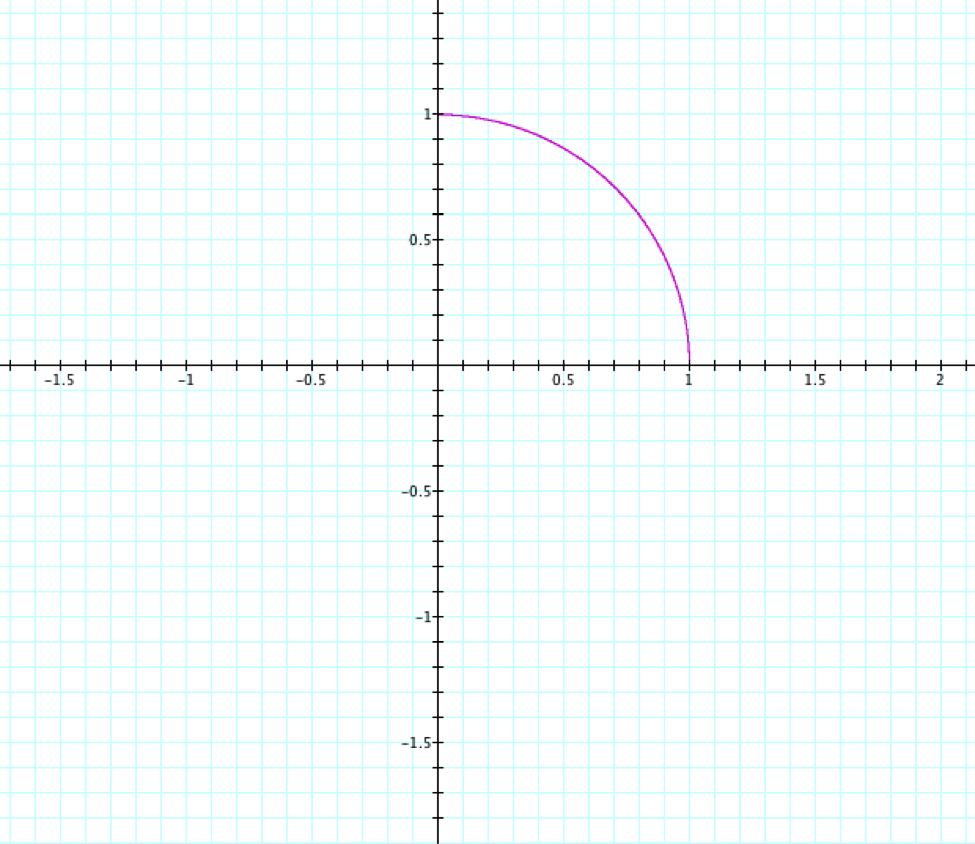
We can create the 4 parts of a circle all four quadrants of the graph simply by changing the range.
t: -0.5...0
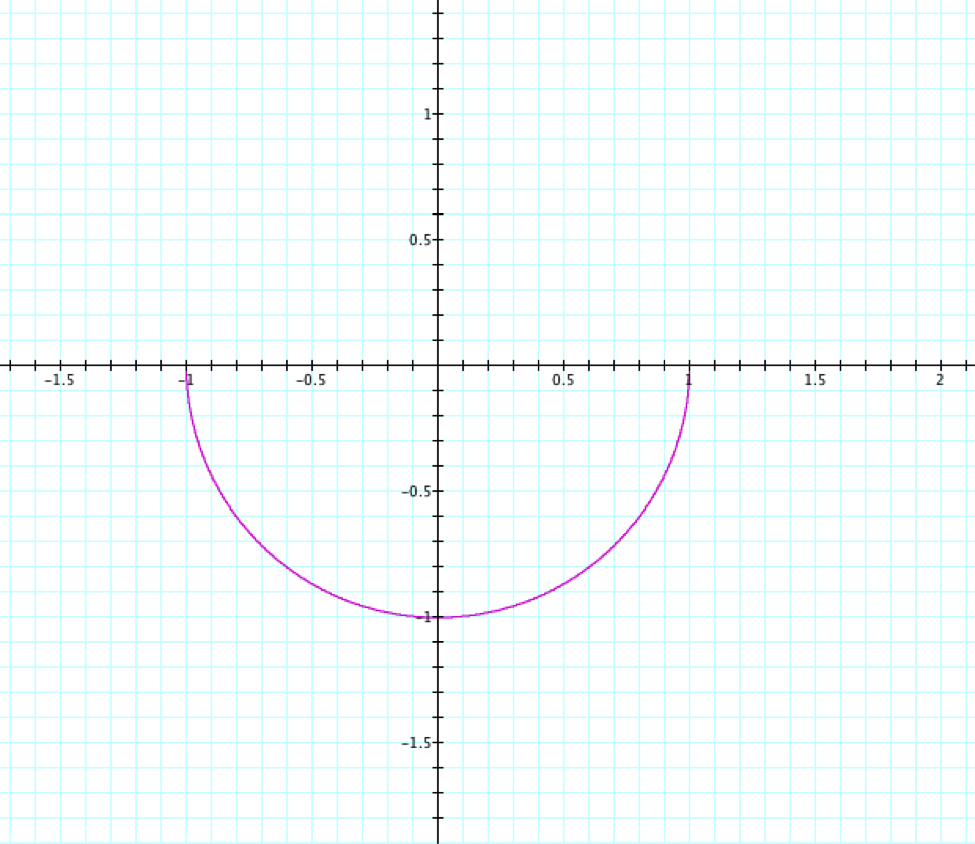
t: 0...-0.25
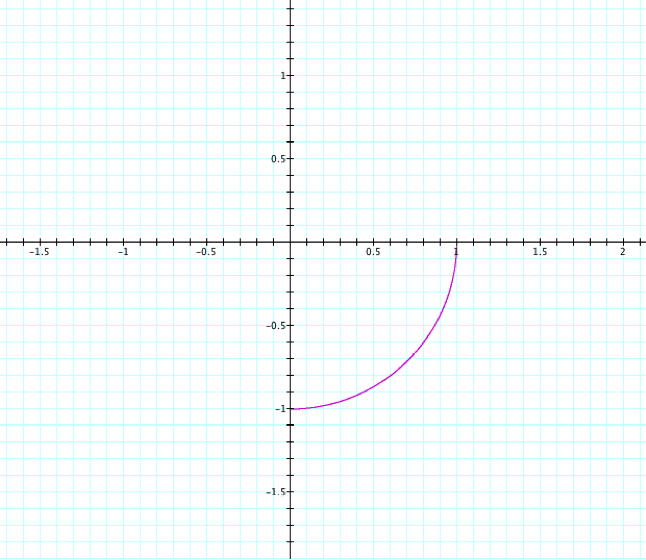
Before I made the next graph, I had it in mind that the quarter of the circle would appear in the III quadrant.
t: -0.25...0

However, it is clearly still in the IV quadrant like the range (t: 0....-0.25) before. This is because the 0.25 creates only 1/4 of the circle. It is not actually a range on the x-axis going from one point to another horizontally.
We can also change the value of 2![]() to another number, leaving the t where it was in the equation.
to another number, leaving the t where it was in the equation.
t: 0...1
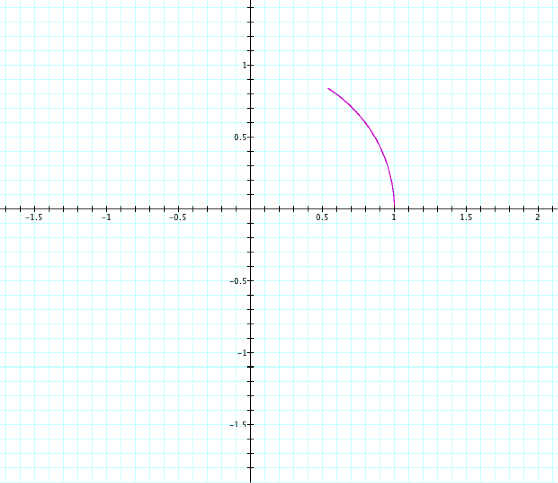
This creates a small curve, but does not create a quarter or half of the circle as seen above.
t: 0...0.25
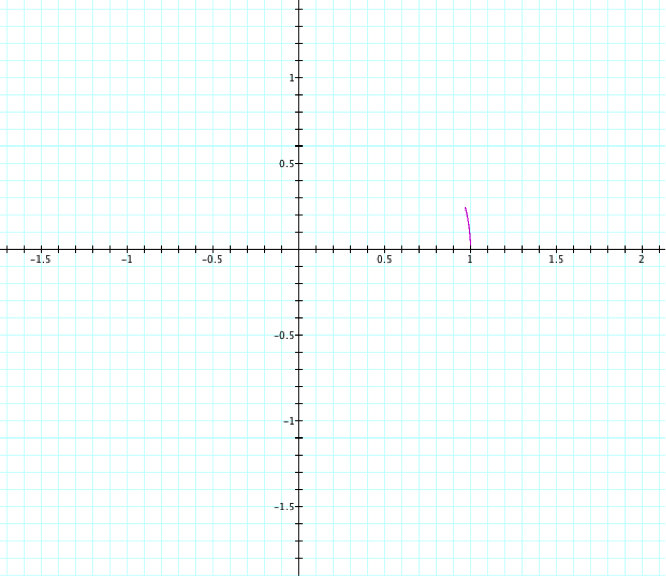
This just shrinks the size of the curve, doing the same thing as changing the range of t in the equations with 2![]() . But since cos1x and sin1x are not the equations of a circle, the curves are smaller in length and do not cover an entire quadrant.
. But since cos1x and sin1x are not the equations of a circle, the curves are smaller in length and do not cover an entire quadrant.