Polar Equations

Elizabeth Nelli

The cool thing about polar equations, is that the graph does not change regardless of the constants being positive or negative. Polar equations are of the form r=a. These will form a circle graph with a center at the origin and a radius of a. Graphs of the form and will have a center on either the x or y axis with a raidius of a. Cos graphs will have a center on the x-axis and sin graphs will have a center on the y-axis. These graphs will obviously only work if a≠0 because a circle cannot have a radius of zero.

For the following graphs, we will be working with a range of : 0...2.

First let's look at the graph of a circle r=1

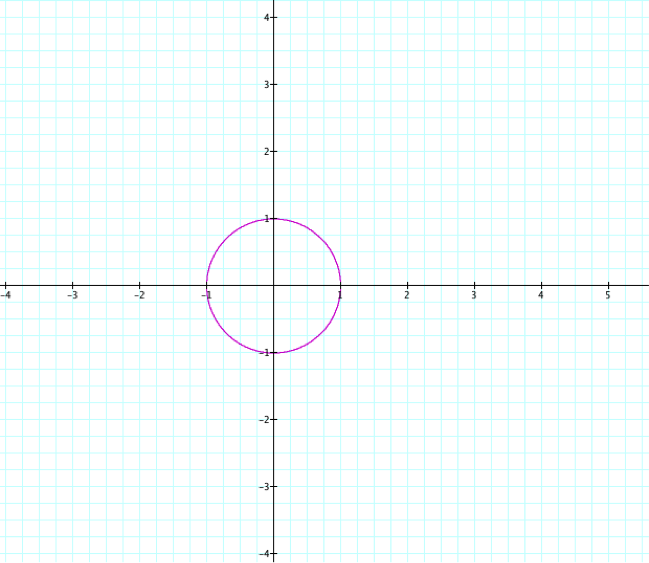
Now we can change the center of the graph by adding sin or cos into the equation. This will have a center on the x-axis with a radius of 3. Can you guess what the equation will be?

Well if you guessed , you were right! Here's the graph.

Now let's move the center to the y-axis, keeping the radius at length 3.

 

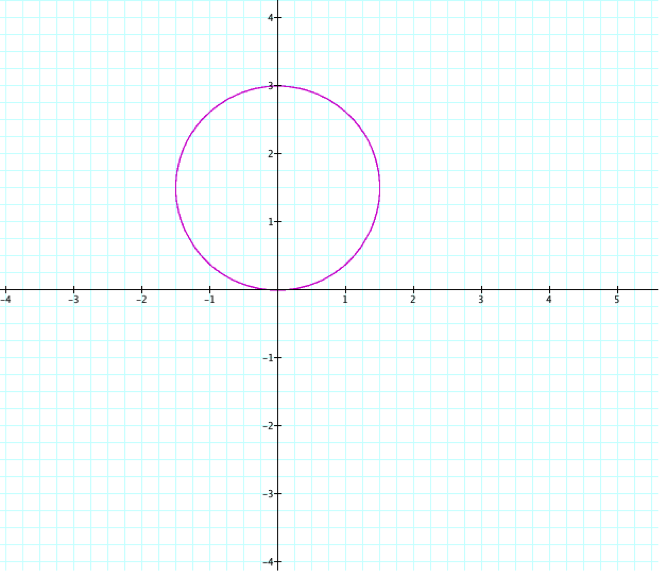
When using  and  we can change the shape of the graph by adding a constant n, to end up with   and , when a,n ≠0. These equations will look like a flower and the “pedals” will vary depending on the value of n. When n is odd, the graph is generated as increases from 0 to and the flower will have n pedals. When n is even, the entire graph is generated as increases from 0 to 2and the flower will have 2n pedals. The size of the “pedals” will vary depending on a.

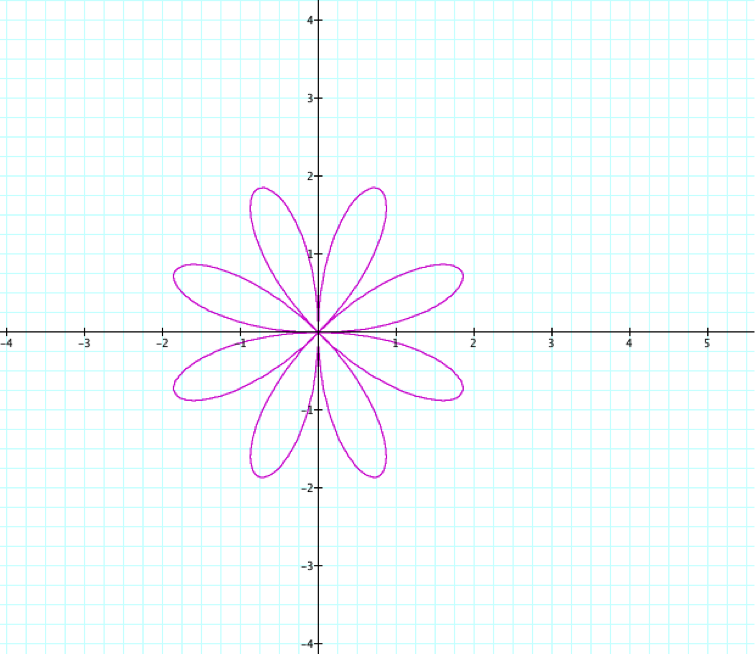
Notice, the graph has 8 pedals because n is even: 2(4)=8.

 

Now using we can see a growth in the size of the pedals.

 

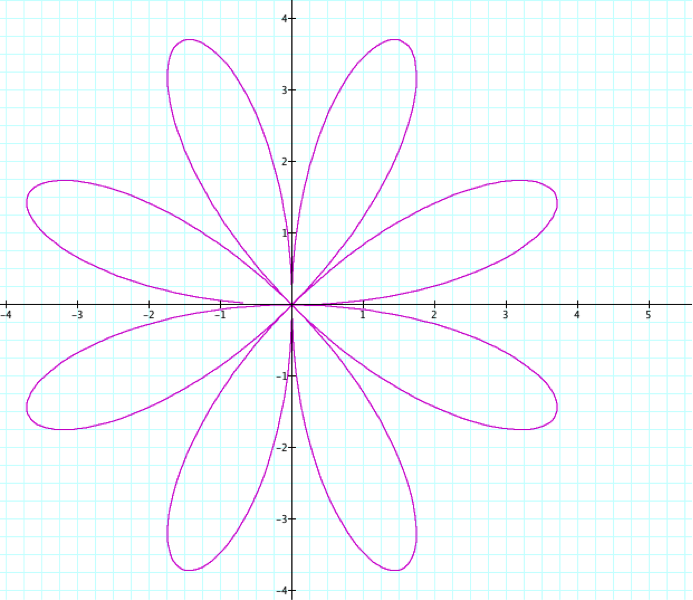
The graphis the same when n or a is either positive or negative.

 

Now let's look when n is odd.

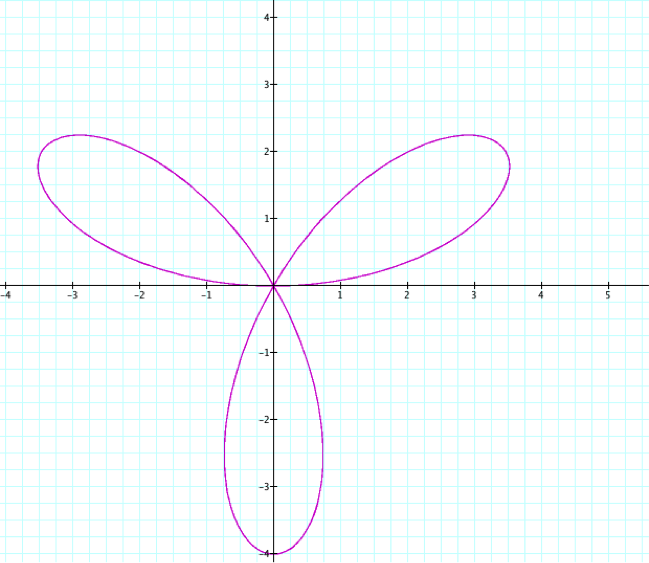
We have 3 pedals because n=3.

Return