Using the JMP Program
Elizabeth Nelli
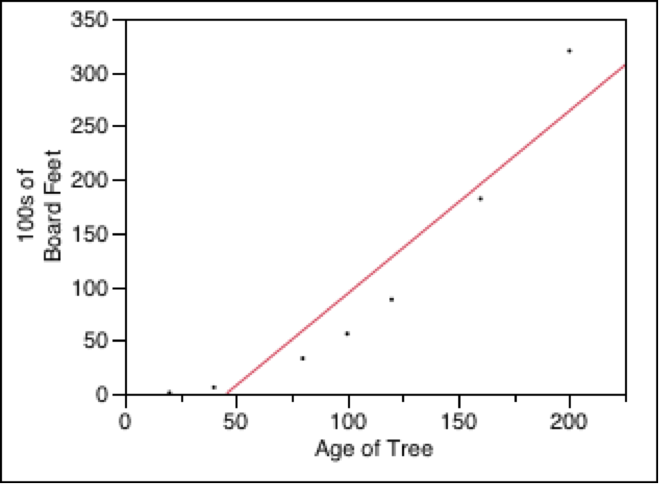
Using the JMP program, I input the data and it came up with the equation of a line to find the number of 100s of board feet per tree. The equation JMP calculated is
100s of Board Feet = -77.85915 + 1.7097418(Age of Tree)
We know that the equation is linear and the correlation between the age of the tree and board feet is strong, we see this in the value of r-squared, which is 0.886148. The closer the value is to 1, the stronger the correlation. This means we can make a very accurate prediction of the board feet per tree using the regression equation.
If we want to fill in the missing spots in the table, we simply plug our information into the equation. For example, using a 60 year old tree we find that the board feet (x) is:
X=-77.85915+1.7097418(60)=24.70593, or 24. Doing this for the remaining points in the graph we get 161 for a 140-year-old tree and 229 for a 180-year-old tree. Now let’s try to predict some other values not on the graph. How about for trees that are 300, 500, and 1000 years old.
| Age of Tree |
100s of Board Feet |
| 20 |
1 |
| 40 |
6 |
| 60 |
24 |
| 80 |
33 |
| 100 |
56 |
| 120 |
88 |
| 140 |
161 |
| 160 |
182 |
| 180 |
229 |
| 200 |
320 |
100s of Board Feet = -77.85915 + (1.7097418)(300)=435
100s of Board Feet = -77.85915 + (1.7097418)(500)=777
100s of Board Feet = -77.85915 + (1.7097418)(1000)=1631
We could also look at this from another point of view. Instead now let’s have the board feet and predict the age of the tree. Pick any arbitrary number, say 368.
368=-77.85915 + (1.7097418)(age of tree)= 260.7757206
How about for a very large number, say 67,459.
67,459=-77.85915 + (1.7097418)(age of tree)=39,501.20372
The new table shows all of our values we have calculated.
| Age of Tree |
100s of Board Feet |
| 20 |
1 |
| 40 |
6 |
| 60 |
24 |
| 80 |
33 |
| 100 |
56 |
| 120 |
88 |
| 140 |
161 |
| 160 |
182 |
| 180 |
229 |
| 200 |
320 |
| 260 |
368 |
| 300 |
435 |
| 500 |
777 |
| 1000 |
1631 |
| 39,501 |
67,459 |