Graphing Transformations

Elizabeth Nelli

In this write-up we will be exploring translations. Translations are isometries, which means they preserve distance. A translation moves each point of the plane the same distance in the same direction. Each translation depends on two constants a and b, so we denote it by ta,b. It sends each point (x,y) to the point (x+a, y+b).

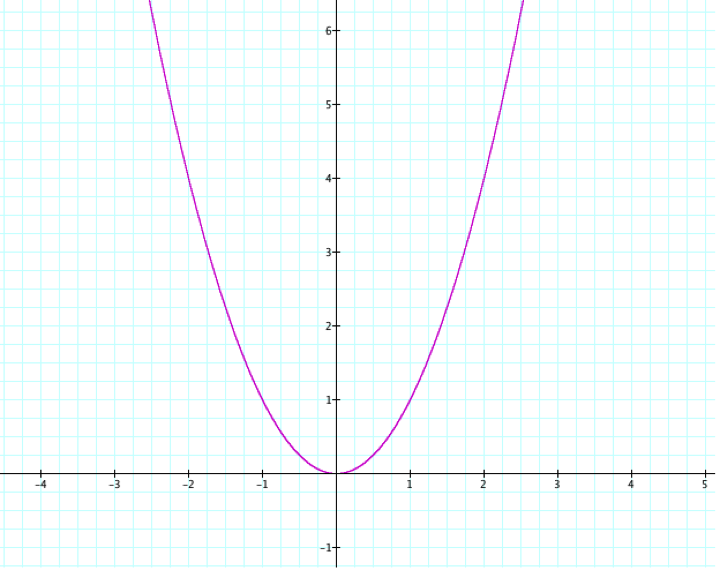
Let’s take a look at the graph
The shape of this graph is called a parabola. It is a symmetrical U-shaped curve. 

Now let’s look at this graph by adding different c values ranging from 3 to -4

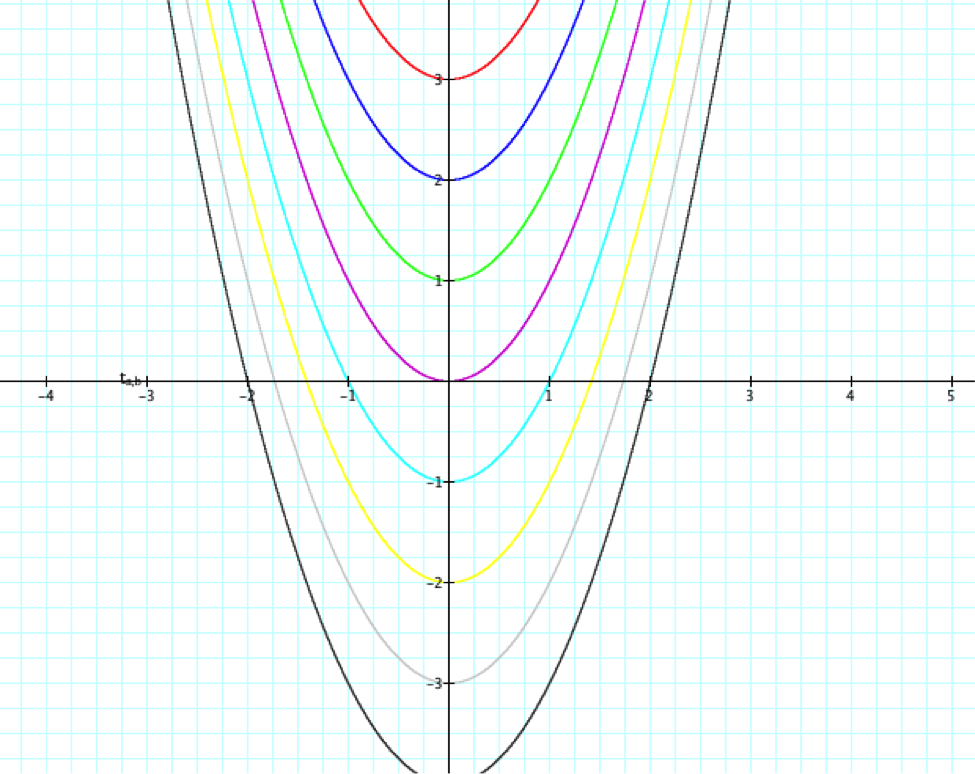
The equations of these graphs in order from top to bottom are:

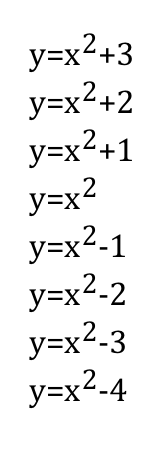
As we can see, the parabola is moving down as the c-value decreases.

Let us prove why this is a translation.
For this proof, let’s use

left x-intercept (-1,0) to right x-intercept (1,0)
  left x-intercept (-2,0) to right x-intercept (2,0)
(-1,0) and (-2,0) will be our first pair

We need to use the distance formula to prove these are an isometry. This means the distance between the two is the same.

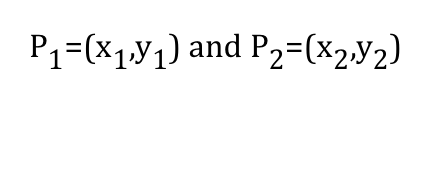
As mentioned earlier, each translation depends on two constants a and b. It sends each point (x,y) to (x+a, y+b).

So we end up withand

Plug andinto the distance formula

we end up with this answer for our first pair:

Now plug in and into the distance formula to get this answer:

so we can see that since the distances are preserved, this is translation