Quadratic Equations

Elizabeth Nelli

Here we see a graph of differing variations of the equation , where a=1 and y=b. The c values range from -5 to 5, in 1 unit increasing order.

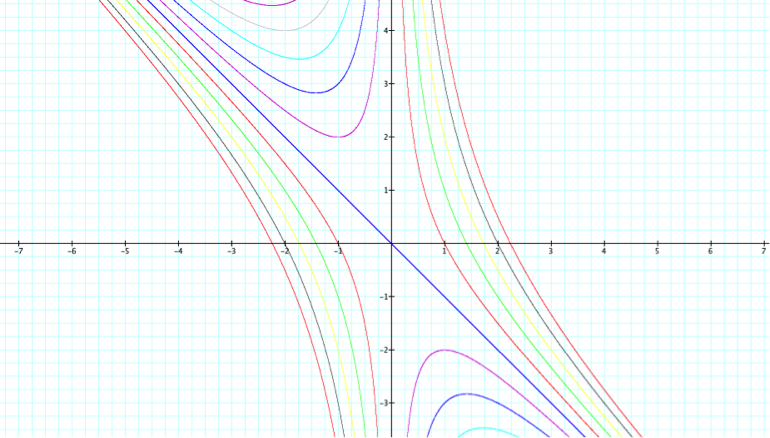
wu3pic1

Now, when we add 2x+b=0 to the graph we get:

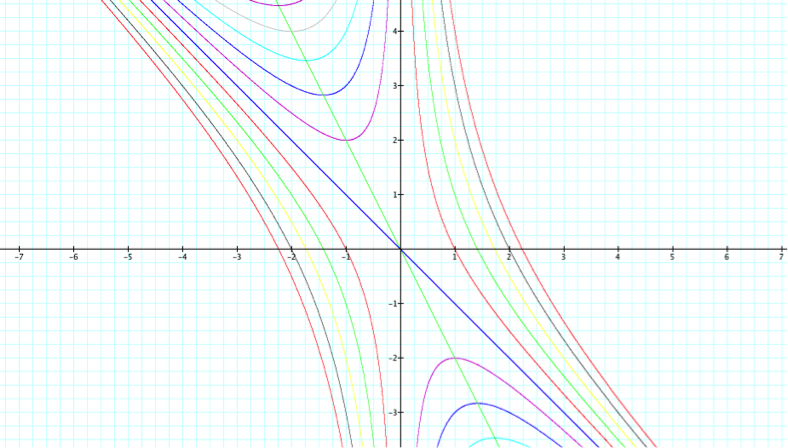
wu3pic2

The green line passing directly through the origin represents this equation. This line passes through the points midway between the sides of each of the hyperbolas, meaning it is the minimum and maximum points on each hyperbola part, where that exists. To obtain this line, we must take the derivative of the above equation (where y=b).

 

Because these lines are hyperbolas, the line x+y=0 and the line x=0 are asymptotes and any horizontal appearing on the graph will intersect the hyperbolas where roots occur.

If we take any horizontal line on the graph, say for example y=2.5, we get this graph.

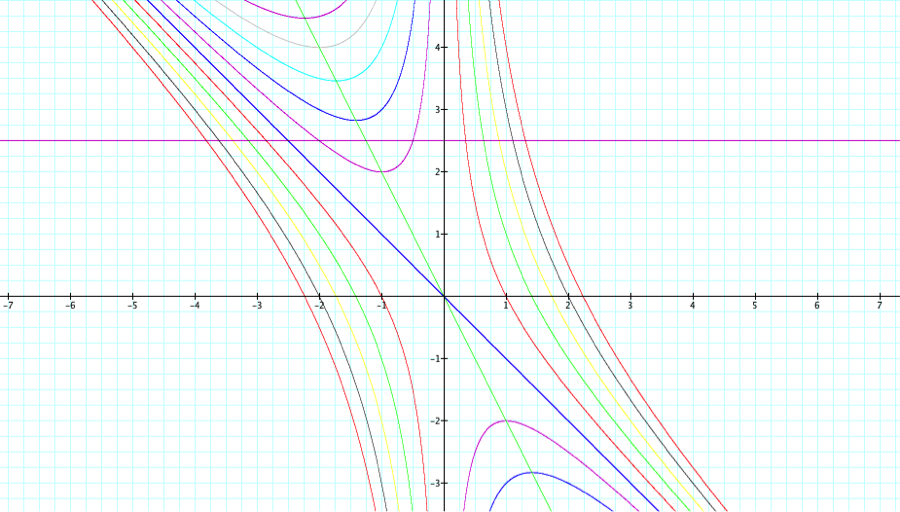
wu3pic3

The intersection of y=2.5 will intersect 2x+b=0 at a point halfway between the two intersections between the parabolas.

Here we see y=2.5 and y=3.25

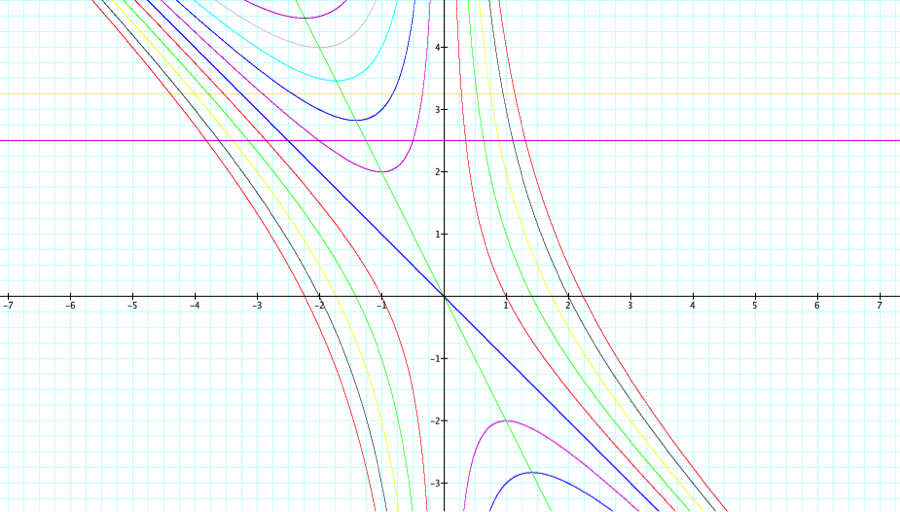
wu3pic4

 

All of these are depictions of roots of the hyperbolas.

We know the quadratic equation is and the quadratic formula is or .   But not all of us know what each part represents graphically.

The represents the point of intersection with a horizontal root line (aka: the midpoint) and the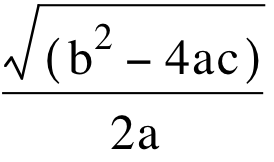or 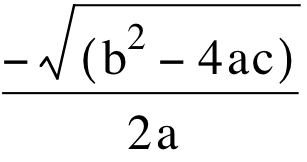represents the distance on either side of the midpoint.

Return