Centroid

Elizabeth Nelli

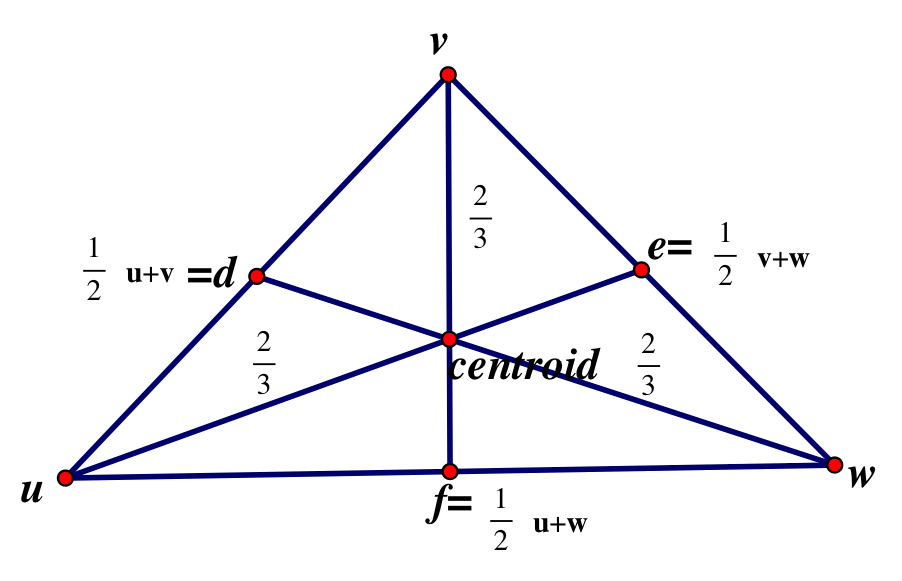
The centroid of a triangle is the intersection of the three medians.
A median of a triangle is a straight line drawn from the vertex of an angle to the middle of the opposite side.

Proof:
Let’s say triangle uwv is made up of the vectors u,v,w,d,e,f. We know by construction that e is the midpoint of v and w, d is the midpoint of v and u, and f is the midpoint of u and w. Therefore, e=1/2(v+w), d=1/2(u+v), and f=1/2(u+w).
By the definition of a median, we know that ue is a median, wd is a median, and vf is a median.

Assume that the centroid lies 2/3 of the way between each angle.
This means that

u + (2/3)((1/2)(v+ w) - u) = u + (1/3)(v + w) - (2/3)u = (1/3)( u + v + w)=
w+ (2/3)((1/2)(u+ v) - w) = w + (1/3)(u+ v) - (2/3)w = (1/3)( u + v + w)=
v + (2/3)((1/2)(w + u) - v) = v + (1/3)(w + u) - (2/3)v = (1/3)( u + v + w)

This means the centroid lies 2/3 of the way between ue, vf, and wd.

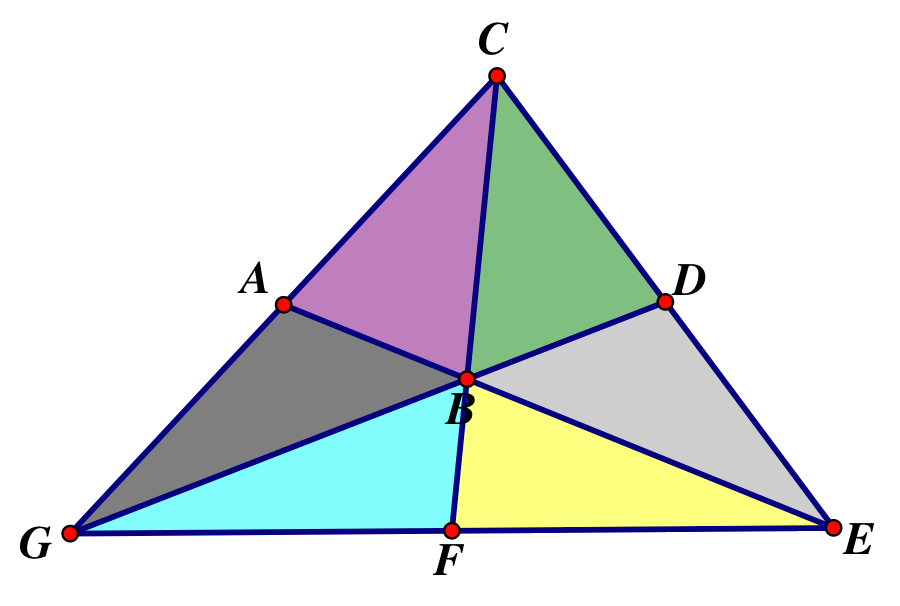
There is also a claim that states the 6 sub triangles formed by the medians with the common point at the centroid have the same area. Using GSP, we can prove this claim with measurements. Note the 6 different triangles formed: ABC, ABG, DBC, DBE, FBE, and FBG.

Based on the above proof, we know that A, D, and F are all midpoints of their respective sides, then we know that CD=DE=AC=AG=FG=FE.
Also, we know that the centroid is 2/3 of the way between CF, EA, and GB, therefore CB=EB=GB.
Lastly, we know that from D, A, and F, to be is equal to ½, therefore AB=DB=FB.
This means that all sides of each triangle are equal; meaning the area of each triangle is equal as well.

Here is a GSP construction and measurements showing this: