Orthic Triangle
Elizabeth Nelli
The orthic triangle is a triangle inscribed in any given acute-angled triangle ABC with minimum perimeter.
Take any triangle ABC and create the altitudes of that triangle
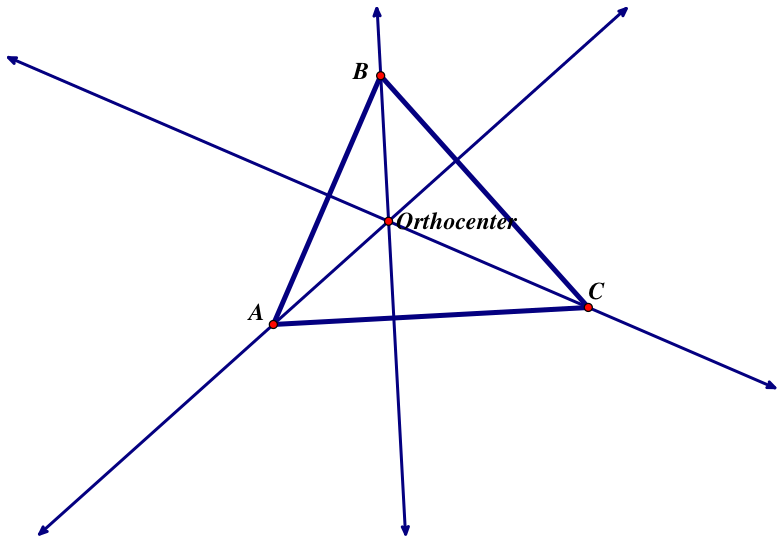
These altitudes meet a central point called the orthocenter
We label the intersections of the altitudes with the angle’s opposite side as A’, B’, and C’ where A’ is the altitude through A that meets side BC, B’ is the altitude though B that meets side AC and C’ is the altitude through C that meets side AB.
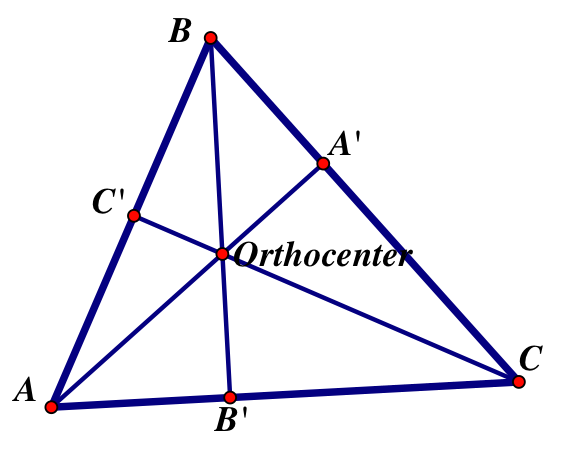
Now by connecting points A’, B’, and C’, we create what is called the orthic triangle.
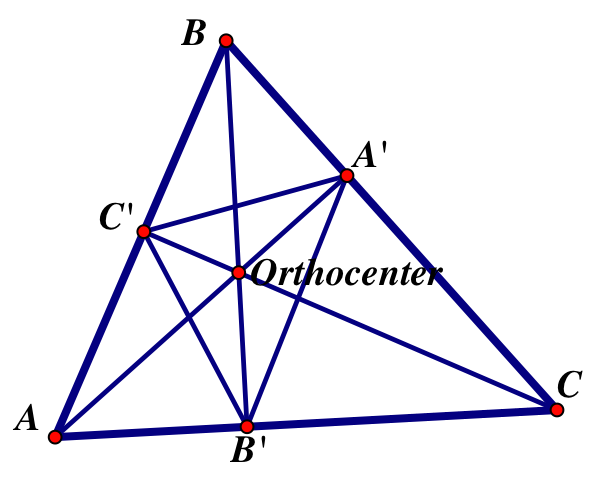
Proof: Construct the triangle with minimum perimeter inscribed in a given triangle
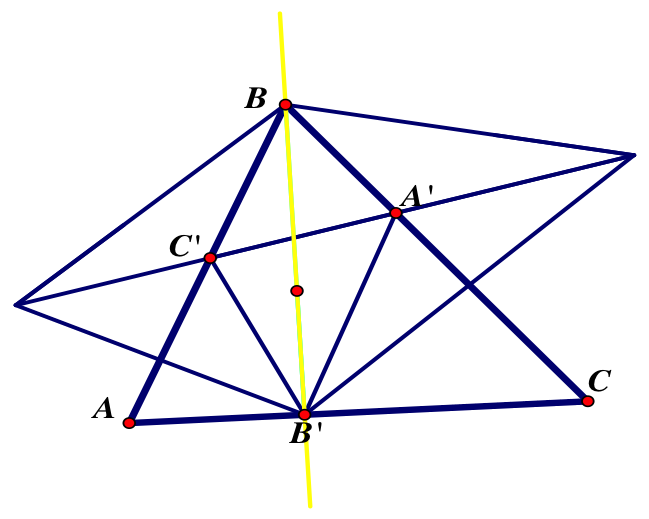
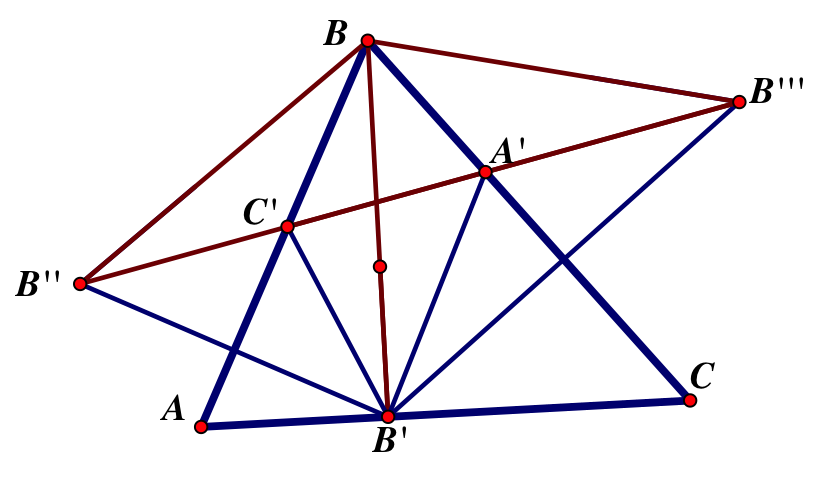
Let’s reflect B’ over each side and label the reflection over AB, B’’ and the reflection over BC, B’’’. Draw a line connecting B’’’ and B’’ through points C’ and A’.
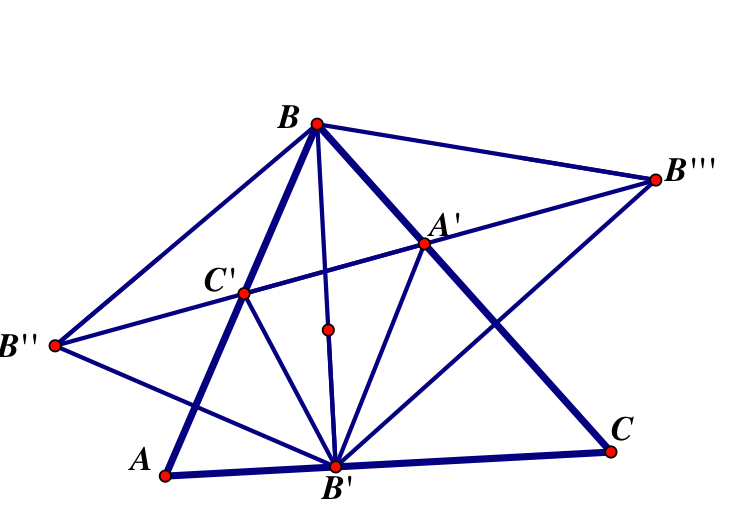
Now |C’B’|=|C’B’’| and |A’B’|=|A’B’’’|
Assume: P(A’B’C’)=A’B’+B’C’+A’C’
= A’B’’’+A’C’+C’B’’
=B’’’A’+A’C’+C’B’’
>B’’B’’” where P is the perimeter (this must be less than or equal to because B’’B’’’ must be at a minimum in order to inscribe a triangle with minimum area. Shown later in the proof).
We know that BB’’=BB’’’ because they are reflections over AB and BC. Therefore triangles BB’B”” and BB’B’’’ are isosceles.
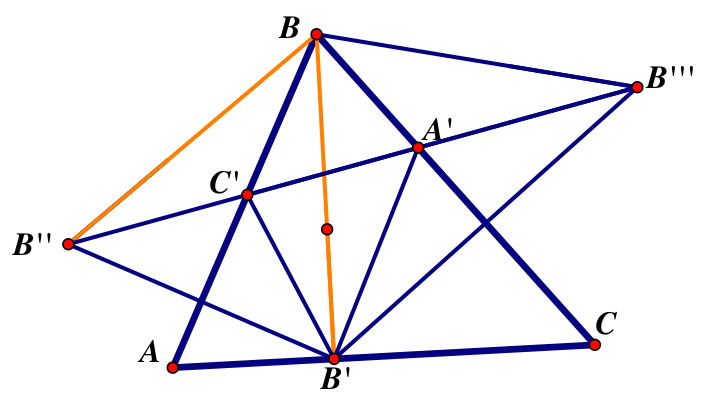
BB’’=BB’
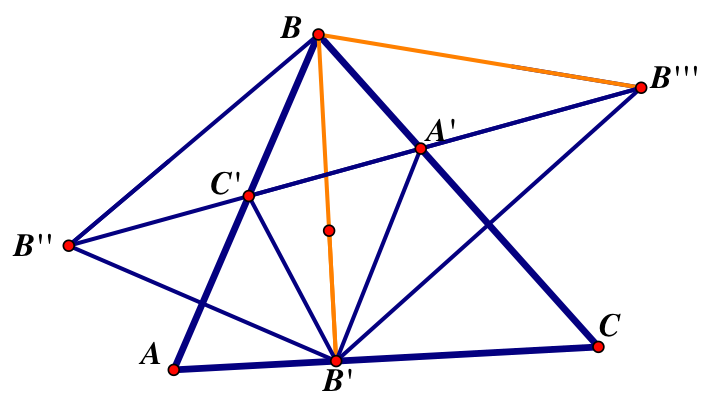
So we know that triangle BB’’B’’’ is also isosceles.
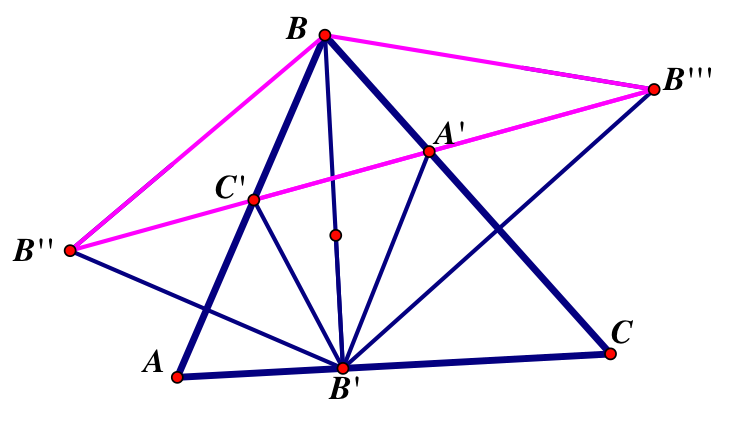
Next we look at angles
< B’’BB’’’=2<B
=2<B’BA+2<B’BC
Therefore, BA is the angle bisector of <B’BB’’ and BC is the angle bisector of <B’BC
We can see that B’A’=A’B’’’ and B’C’=C’B’’
Because we know that B’’BB’’’ is isosceles and directly proportionate to B’B, then when B’B is at a minimum so is B’’B’’’. In order to find the minimum triangle that can fit inside ABC we have to find where B’’, C’, A’ and B’’’ lie straight line. When they do B’’B’’’ will be at a minimum. Since, by construction, I connected a line from B’’’ to B’’ through points A’ and C’, then B’’, C’, A’, and B’’’ all lie on a straight line, meaning that B’’B’’’ is at its minimum.
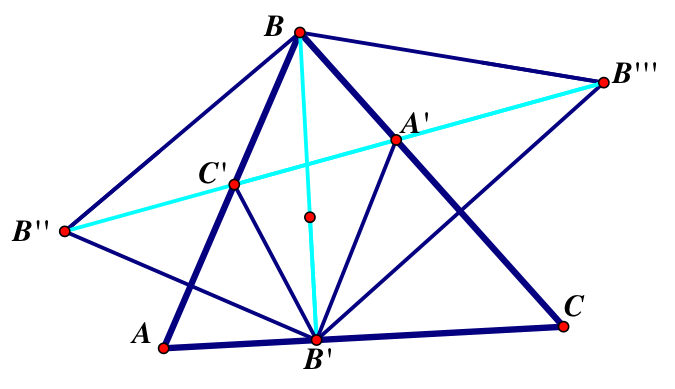
We know that the minimum of BB’ is the attitude of <ABC through segment AC. Therefore the minimum sides of the triangle A’B’C’ are formed by all the altitudes of the triangle ABC, thus the orthic triangle is the triangle with minimum perimeter inscribed in any given triangle.