

Tangent Circles: Steiner Chain
Elizabeth Nelli
A Steiner Chain is made using 2 non-intersecting circles and creating a set of n-circles which are tangent to the previous and next circle in the set as well as tangent to the two original circles. There are several different ways to create a Steiner Chain; some contain n-circles of equal size while others contain n-circles in which none are equal. There are closed Steiner Chains and open Steiner Chains. To be a closed Steiner Chain means that the first and last of the n-circles must also be tangent to each other. When a Steiner chain is open, these circles do not have to follow this rule. In some Steiner Chains, all n-circles are inside of the larger of the two original circles while in other chains, there is a combination of circles both in and outside of the larger original circle. I have created one Steiner Chain for this write up. It is the most commonly seen Steiner Chain. It is closed and all the circles are of the same size.
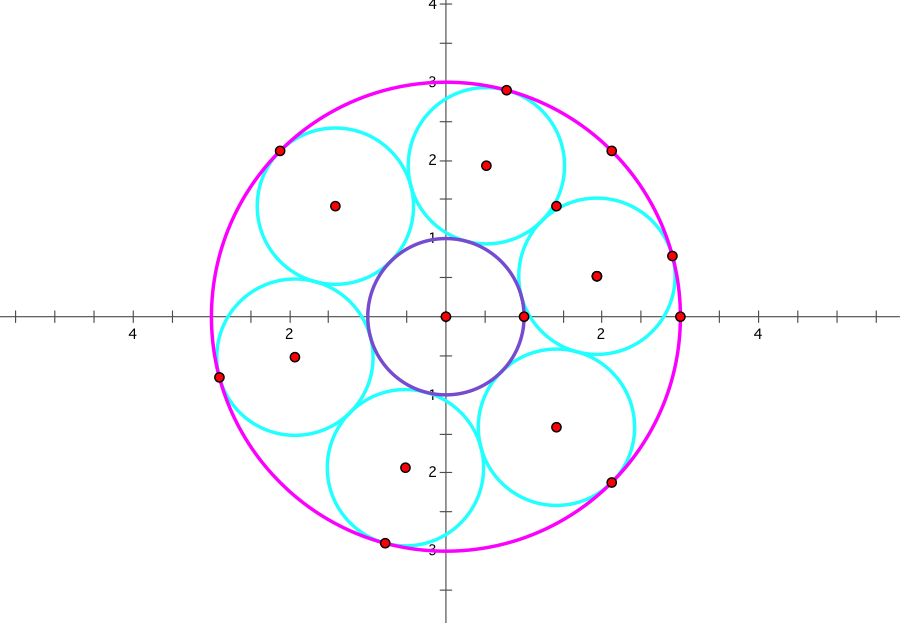
First, I chose my n to be 6. Then I used the formula ![]() . From there, I plugged my 30 into the formula
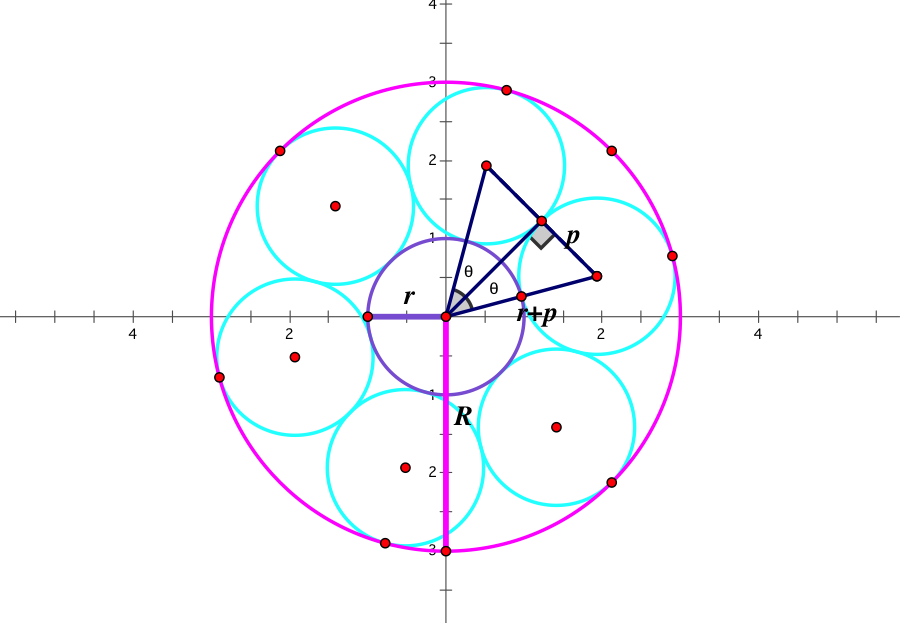
. From there, I plugged my 30 into the formula ![]() and got that r=1 and p=1. From this, I wanted to find out what the radius of my large circle would be, so I used the formula R=r+2p, to get that R=3. And then I began with the construction. I knew the centers of my circle had to be equidistant from eachother, and had to be r+p distance from the center of the smaller circle. Therefore, at 60 degrees apart, my centers lie on the points (on a polar grid) at (2, 15), (2, 75), (2, 135), (2, 195), (2, 255), and (2, 315).
and got that r=1 and p=1. From this, I wanted to find out what the radius of my large circle would be, so I used the formula R=r+2p, to get that R=3. And then I began with the construction. I knew the centers of my circle had to be equidistant from eachother, and had to be r+p distance from the center of the smaller circle. Therefore, at 60 degrees apart, my centers lie on the points (on a polar grid) at (2, 15), (2, 75), (2, 135), (2, 195), (2, 255), and (2, 315).
We can technically pick any n and use all these formulas to create another Steiner Chain. However, say you want to pick n=4, then our ![]() value is 45 degrees, meaning that
value is 45 degrees, meaning that ![]() . This means
. This means ![]() , which gives us
, which gives us ![]() . This ends up being a very nasty number for our value of r. Which is why creating a Steiner circle of this type only works when n=6.
. This ends up being a very nasty number for our value of r. Which is why creating a Steiner circle of this type only works when n=6.