

Locations of the Pedal Point
Elizabeth Nelli
Below is a construction of a pedal triangle. Point P is the pedal point, and can be located anywhere on the same plane as triangle ABC.
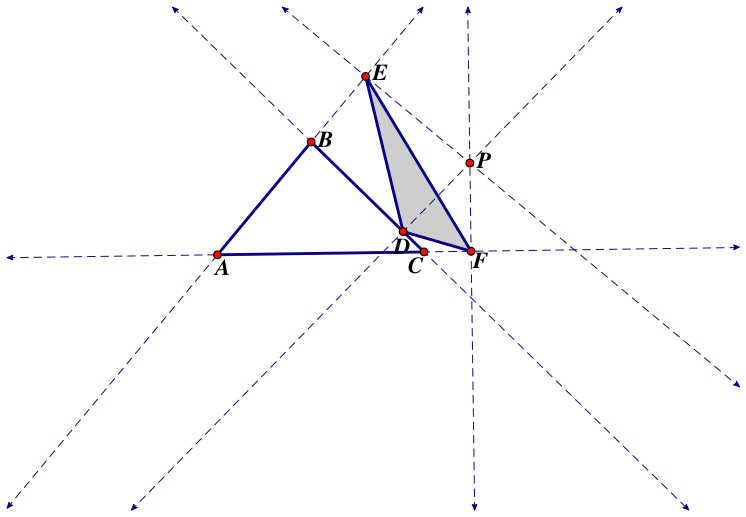
Now let’s look what happens when we move the pedal point so that it is inside DEF.
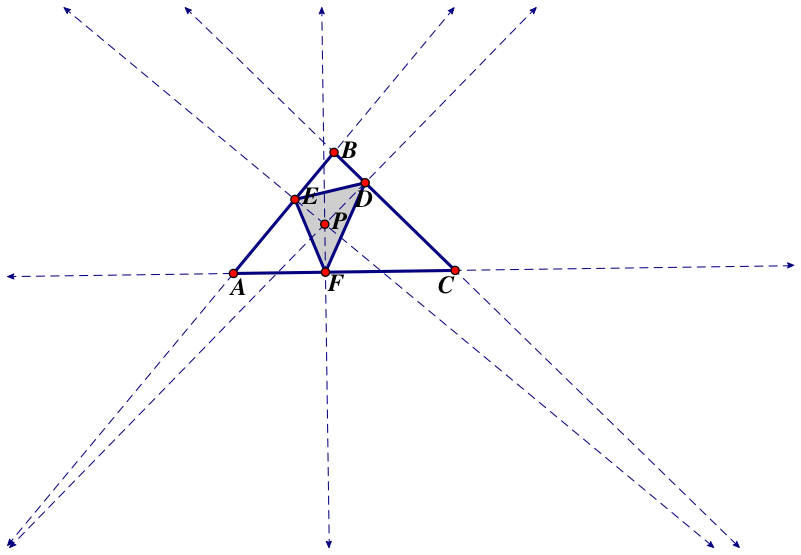
We can see that triangle DEF moves inside of triangle ABC, which is true for all acute triangles because an equilateral triangle will always be acute (since all 3 angles have to be equal and the angles of a triangle add up to 180).
Now, since this triangle is equilateral, we also must see what happens to DEF when ABC is either obtuse or a right triangle.
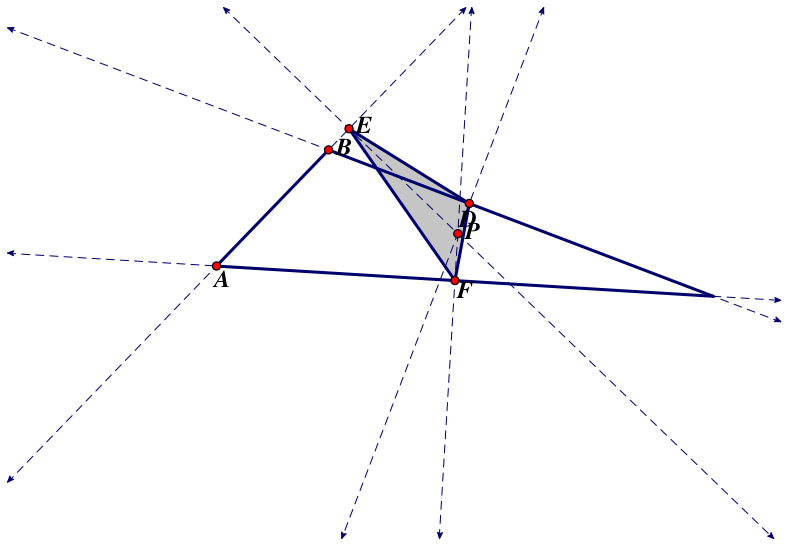
When ABC is obtuse, parts of DEF are outside of ABC when P is inside of DEF.
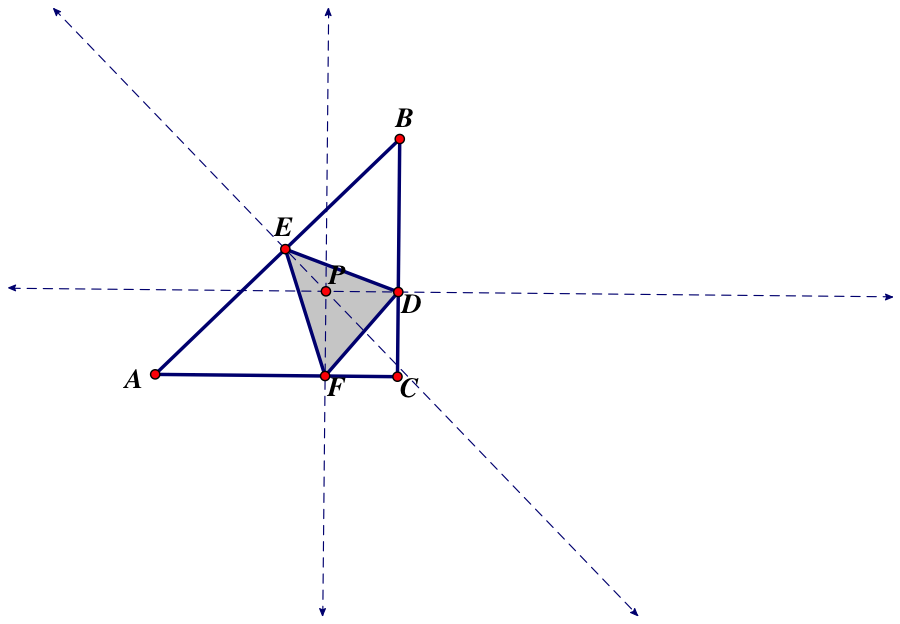
When ABC is a right triangle, and P is inside DEF, then DEF is also inside of ABC
When P is outside of DEF, then DEF is degenerate (meaning it collapses into a line). There is another case like this involving the circumcirle, which will be discussed later.
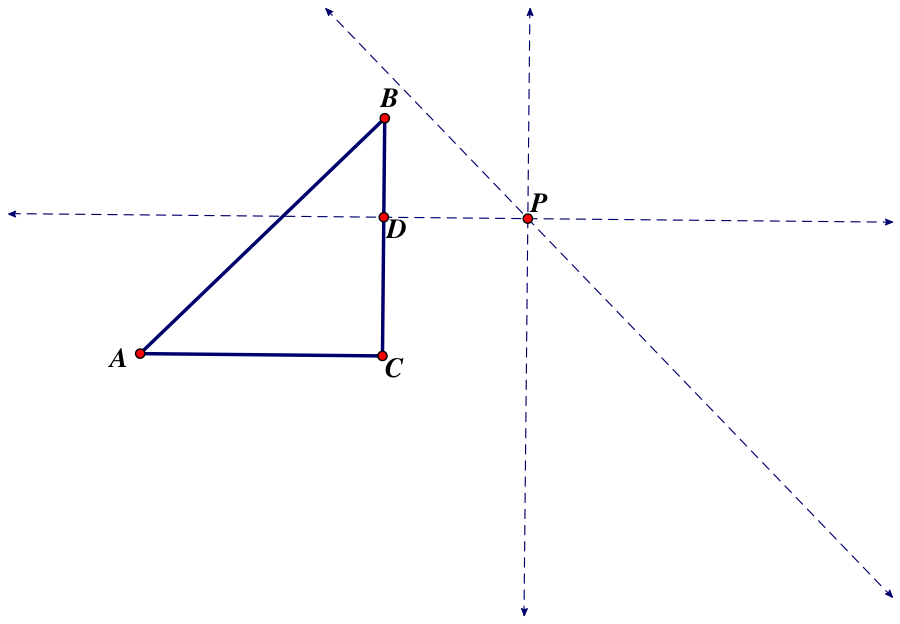
This leads us to wonder where exactly does P fall in regards to the centers of triangle ABC.
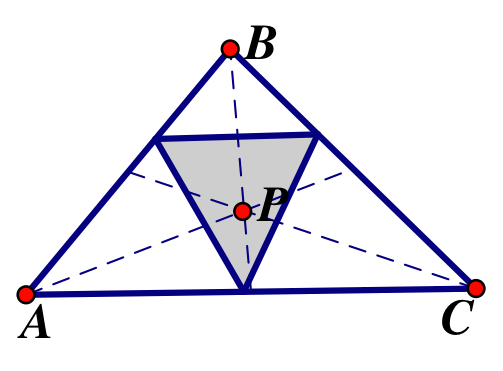
First let’s take a look at the centroid of an acute triangle ABC
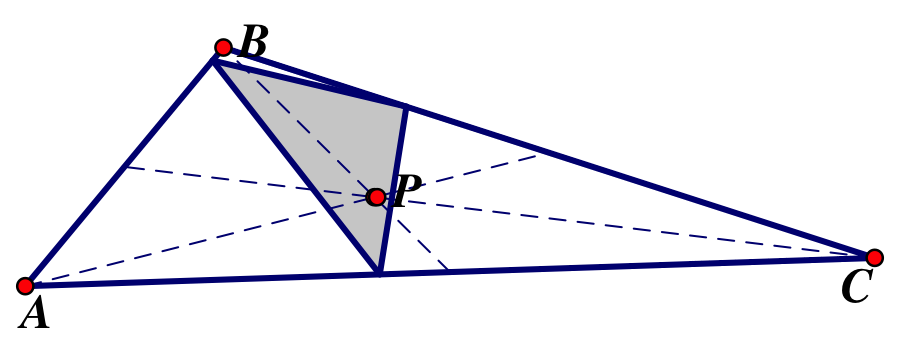
When ABC is obtuse
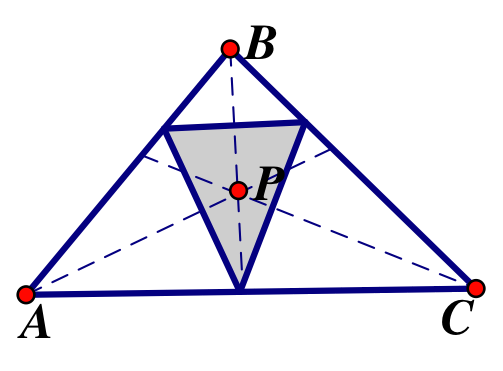
Now let’s look at the incenter when ABC is acute.
Now the incenter when ABC is obtuse.
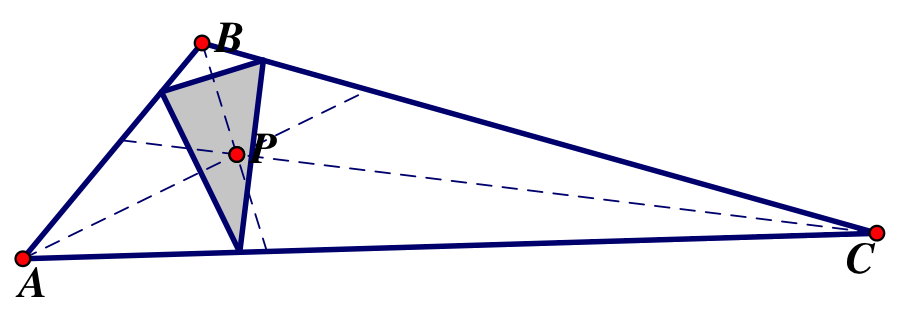
This triangle is known as the intouch triangle.
Now let’s look at the circumcenter
Here is what happens when the circumcenter is inside of ABC
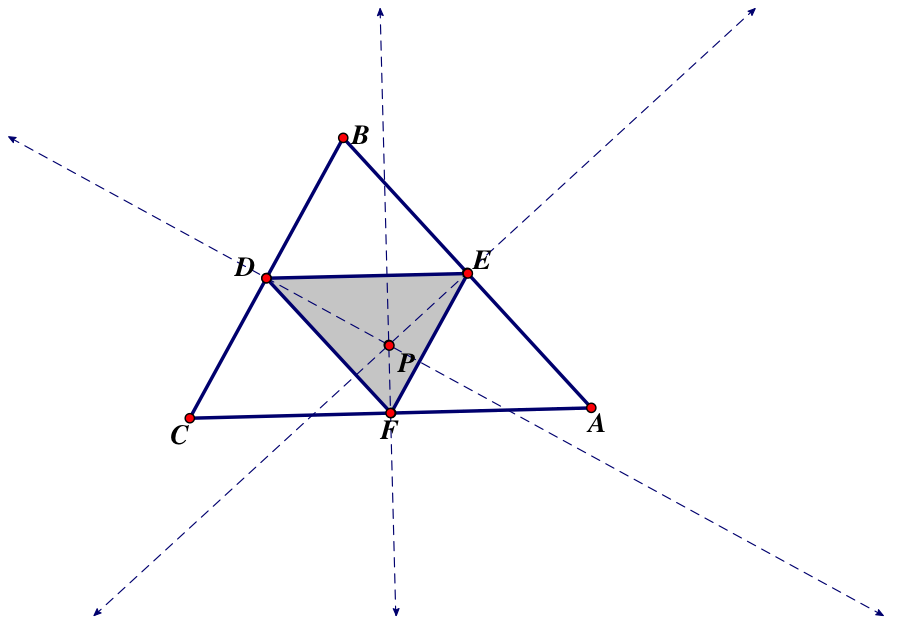
As you can see, all the vertices of DEF lie on the midpoints of the sides of ABC.
Here is what happens when the circumcenter is outside of ABC
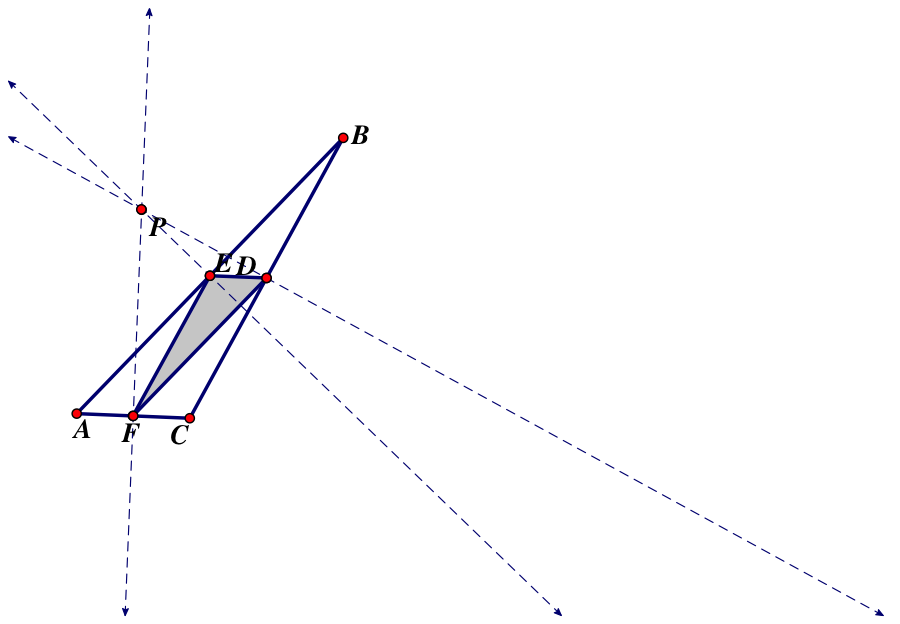
Again, all of the vertices of DEF lie on the midpoints of the sides of ABC.
This triangle is called the medial triangle because it lies on all the medians of the triangle for which it is inscribed. Regardless of whether the pedal point falls inside or outside of the triangle ABC, DEF’s vertices will always lie on the mid-points of the sides of ABC.
If P is on the circumcirle of a triangle, then DEF collapses into a line called the Pedal line (aka Simpson line).
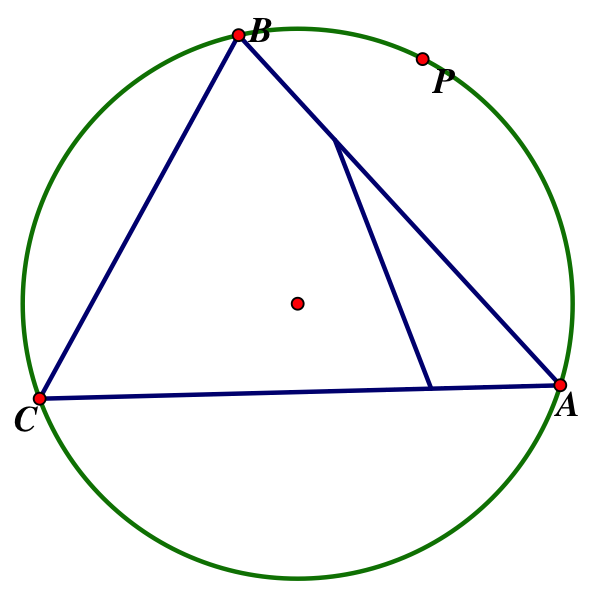
And finally we look at the orthocenter
Here is what happens when the orthocenter is outside of an obtuse ABC. We can see again that DEF is degenerate.
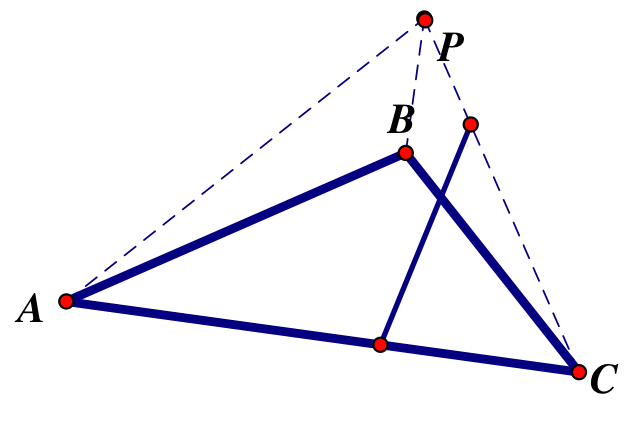
And when it is outside of an acute ABC. Again, DEF is degenerate.
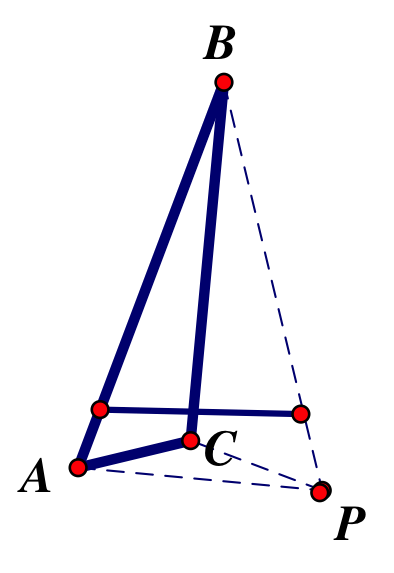
Here is what happens when the orthocenter is inside an obtuse ABC
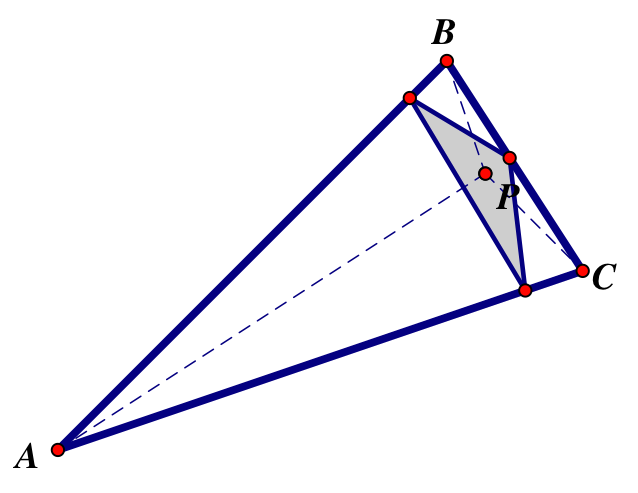
And when it is inside an acute ABC
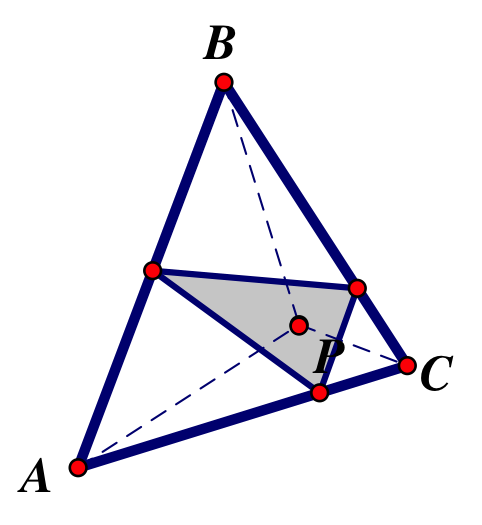
This triangle is the orthic triangle.
DEF is clearly visible in both an acute and obtuse triangle ABC when the orthocenter is located inside ABC. However, when the orthocenter falls outside of the side lengths of ABC, then DEF is degenerate.