Bouncing Barney

Does the path create similar triangles?
3 of the 4 triangles are congruent and the fourth is similar. This fourth triangle is larger in size and “flipped” upside down based on its angles. So basically all the four angles are congruent when measuring their angles, but they are not congruent based on their side lengths.

 

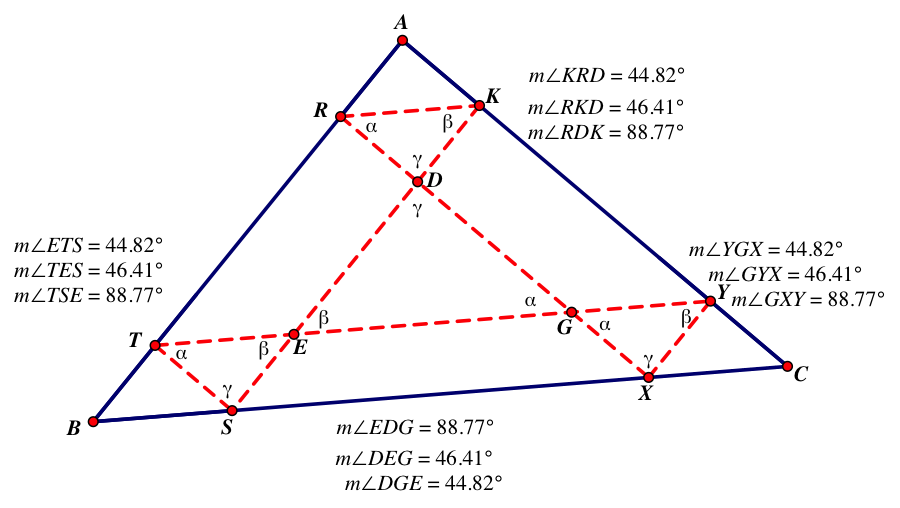
Will he always return to the same starting point? Where does his starting point create congruent triangles?
When he starts 1/3 of the way on side BC, Barney’s path will create 3 congruent triangles.

Triangle ABC is made up of smaller triangles. Because of the properties of parallel and transversal lines, we get that

 

Using this triangle, I can figure out the angles of the remaining triangles to get:

 

When using the sketch of Bouncing Barney and using the formula from above, we can conclude that when Barney starts inside the triangle, he will always end up at the same place. Using measurement tools in GSP, I found that regardless of where Barney's starting point on BC is, he will always travel the same distance to return to his original spot. While the distances before he reaches a wall are not fixed, the total distance Barney travels is constant.

 

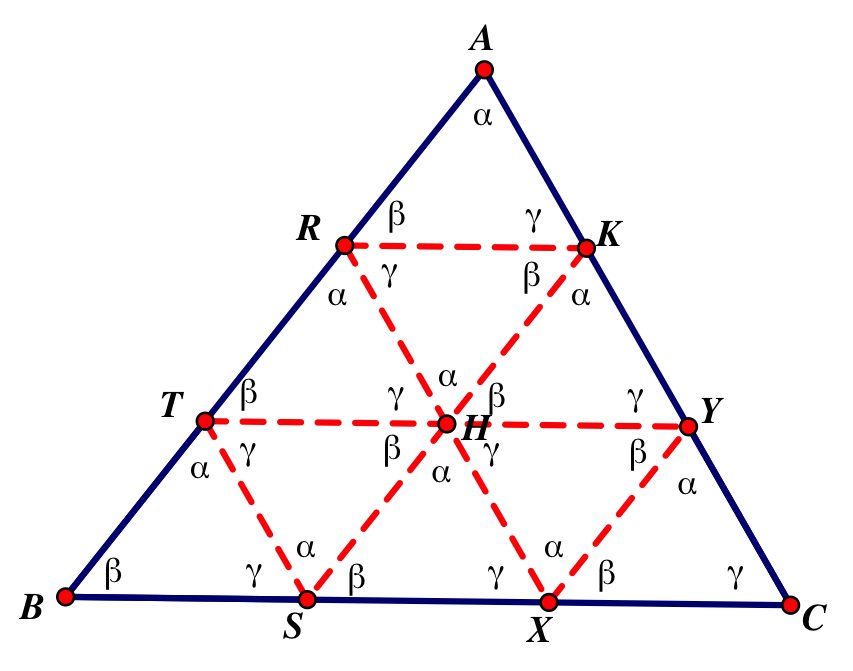
What if the starting point was at the centroid?
If he begins at the centroid, he will make only one triangle path before he returns to his starting point S. This makes sense because the centroid is the center of the triangle. This also makes sense that he will make only one more triangle because if he starts at the center, he will have to change directions each time he hits a wall (side of the triangle), which in this case would be twice because Barney will never reach side BC.

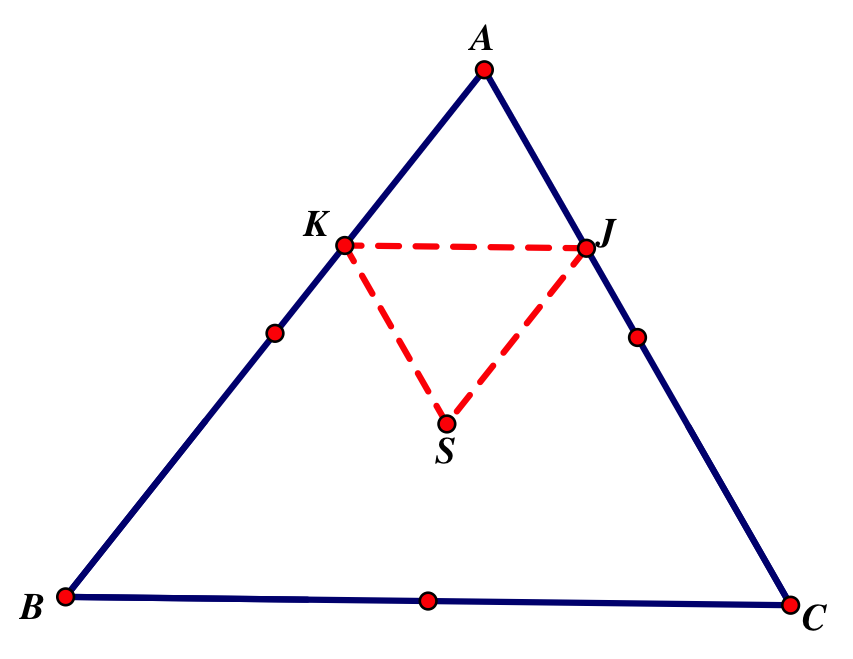
What if Barney’s starting point was at the orthocenter?
Again, Barney will make a path of 3 congruent triangles and 1 similar triangle in the middle that has the same angle measures with different side lengths that returns to his starting point.

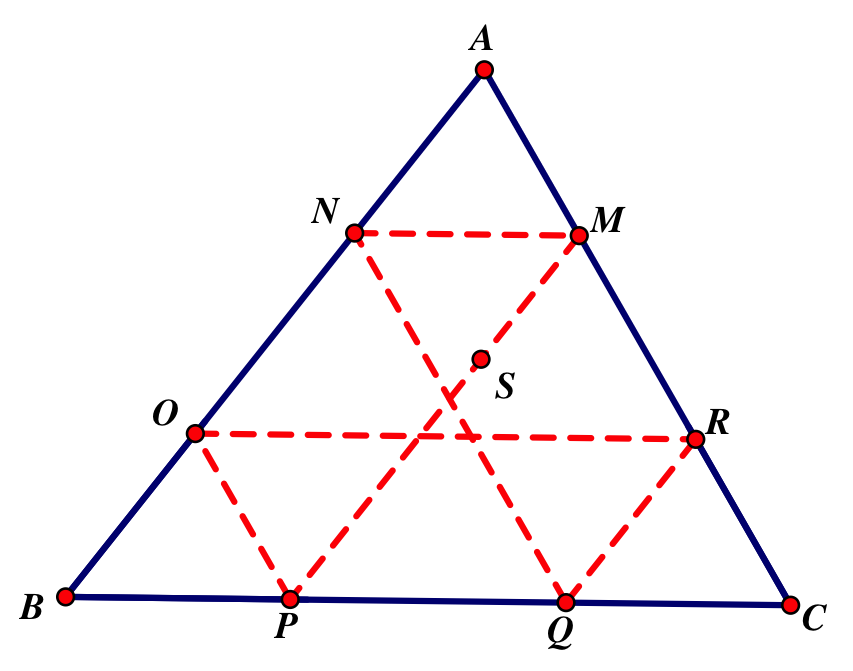
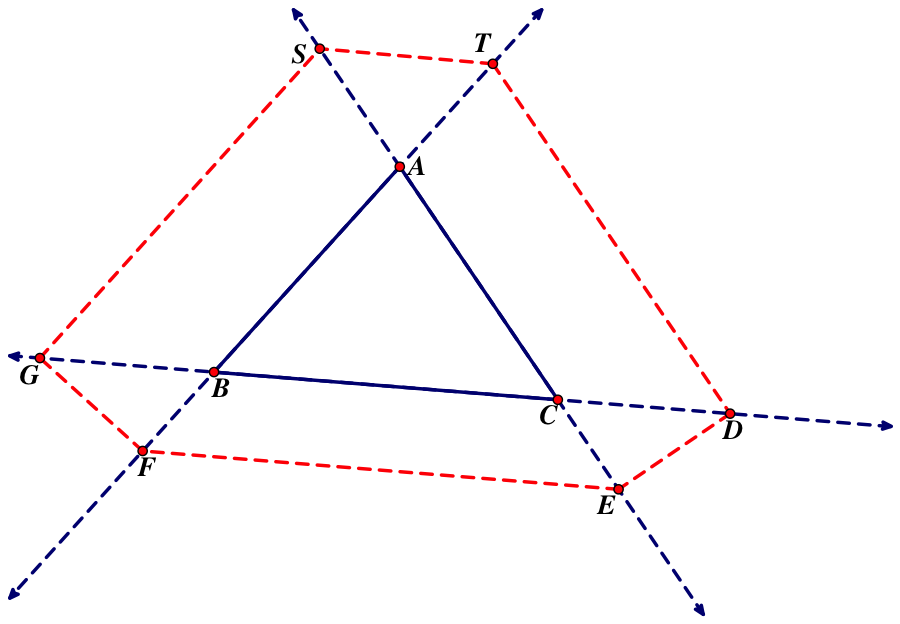
When Barney starts outside of the triangle?

We have to extend the sides of the triangle so that Barney can "bounce" off the walls and switch directs. As you can see, he still will end up at his starting spot, S. He is walking parallel to AB, hits the wall at G, and starts walking parallel to AC. He then hits the wall at F and starts walking parallel to BC. He hits the wall at E and starts walking parallel to AB again. He hits the wall at D and walks parallel to AC again. He hits the wall at T and returns to S, walking parallel to BC.

 

 

 

 

 

 

 

Summary of Fit

RSquare 0.807102

RSquare Adj 0.796386

Root Mean Square Error 6.36631

Mean of Response 21

Observations (or Sum Wgts) 20

Just as with the tree write up from Assignment 12, I just JMP again to calculate the regression equation of the price increase of stamps each year.

The regression equation is Rate (in cents) = -1038.212 + 0.5350502(year)

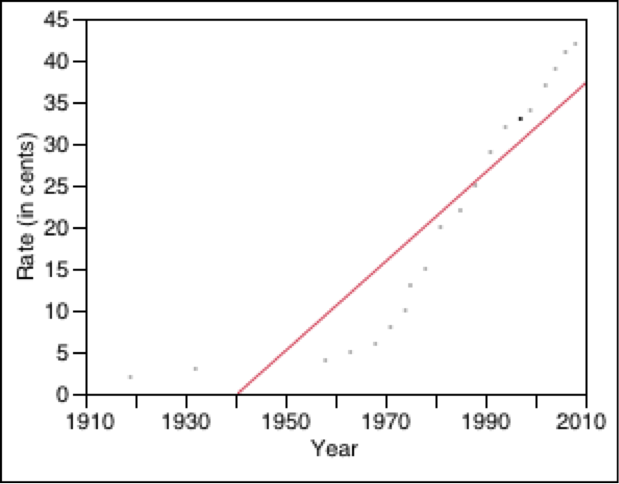
Year	Rate (in cents)
1919	2
1932	3
1958	4
1963	5
1968	6
1971	8
1974	10
1975	13
1978	15
1981	20
1985	22
1988	25
1991	29
1994	32
1997	33
1999	34
2002	37
2004	39
2006	41
2008	42

If we want to find when the price will reach a dollar, we simply plug in 100 to the rate in cents.

100=-1038.212 + 0.5350502(year) = 2127

If we wanted to find out when a stamp would cost 64 cents, we just plug 64 into our equation: 64 = -1038.212 + 0.5350502(year)= 2059

What would be the price of a stamp in the year 3000? x= -1038.212 + 0.5350502(3000) =566 or $5.66

With a correlation coefficient (r-squared) of .807, we can see there is a strong linear correlation between the year and the increase in stamp price.

Year	Rate (in cents)
1919	2
1932	3
1958	4
1963	5
1968	6
1971	8
1974	10
1975	13
1978	15
1981	20
1985	22
1988	25
1991	29
1994	32
1997	33
1999	34
2002	37
2004	39
2006	41
2008	42
2059	64
2127	100
3000	566