

Kristin Ottofy
Assignment 10
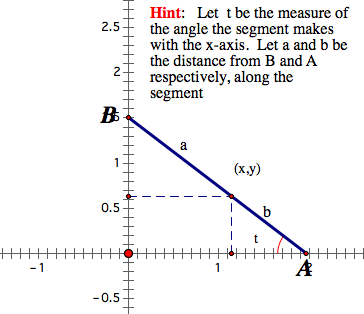
9. Derive the parametric equations for the locus of a point (x, y) on a line segment that is moved so that one end is on the x-axis and the other end is on the y-axis.
Given the following triangle:
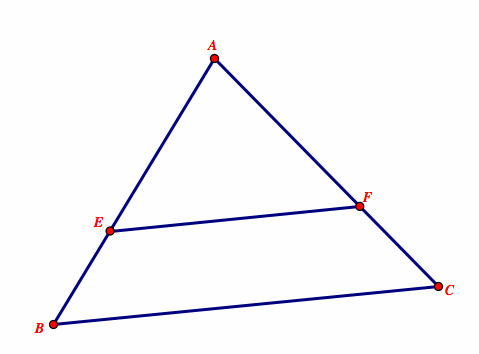
Thales' theorem states that is EF is parallel to BG, then AE/EB = AF/AC.
Here, I have recreated this assignment's triangle and added some notation: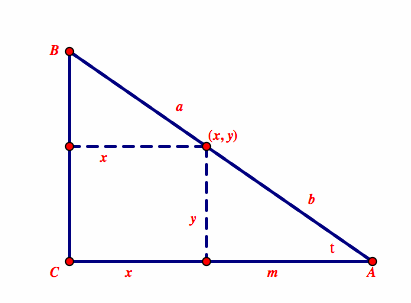
By Thales' Theorem, b/a = m/x. So, bx = am.
Therefore, x = am/b = a*(m/b) = a*cos(t) since cos(t) = m/b.
Also, sin(t) = y/b. So, y = b*sin(t).
Thus, the parametric equations are:
x = a*cos(t) and y = b*sin(t).