

Kristin Ottofy
Assignment 2
2. Fix the values for a and b, vary c. Make at least 5 graphs on the same axes as you vary c.
Let a = 1 and b = 1. Here are the graphs for when c = -2, -1, 0, 1, and 2.
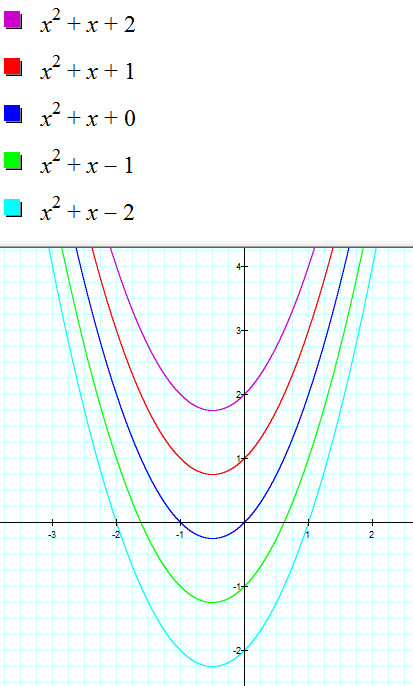
In this case, by varying c, we are translating the parabola vertically. This is seen in by looking at the y-intercepts, (0, 2), (0, 1), (0, 0), (0, -1), and (0, -2), respectively. Here, we can see that if a=b=1, then c is the y-intercept.
Looking at this graph where a=3 and b=-2, we can see that this conjecture holds.
Proof:
(x2+x+c) - (x2+x+(c-1)) = c - (c-1) = 1
Thus, we are translating by the absolute difference between the two c values. The sign of the difference will tell the direction to translate.