Kristin Ottofy
Assignment 4
1. The CENTROID of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
Use Geometer's Sketchpad (GSP) to Construct the centroid and explore its location for various shapes of triangles.
Prove the three medians of a triangle are concurrent and the centroid is 
the distance from a vertex to the midpoint of the opposite side.
Let's look at the following triangle:
To show that the three medians, line segments AD, BE, and CF are concurrent at point H, we need to show that
by Ceva's Theorem.
Using GSP, we can see that
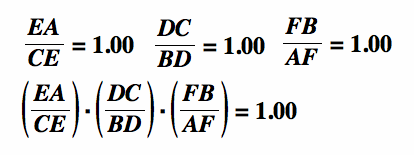
Thus, the three medians of a triangle are concurrent.
Now to show the centroid is the distance from a vertex to the midpoint of the opposite side:
Suppose that the triangle is constructed using vectors where G, H, I, J, K, and L are vectors.
Then,
L = (1/2)(G + K),
J = (1/2)(K + I), and
H = (1/2)(I + G) using vector addition and averages.
Since (2/3)rds has already been suggested to us, let's guess that the centroid does occur (2/3)rds of the way from I to L, K to H, and G to J.
Thus,
I + (2/3)((1/2)(G + K) - I) = I + (1/3)(G + K) - (2/3)I = (1/3)( I + G + K)
which equals
K + (2/3)((1/2)(I + G) - K) = K + (1/3)(I + G) - (2/3)K = (1/3)( I + G + K)
which also equals
G + (2/3)((1/2)(K + I) - G) = G + (1/3)(K + I) - (2/3)G = (1/3)( I + G + K).
Therefore, the centroid lies rds of the way between I and L, K and H, and G and J.