This investigation begins with the following problem.

Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

 

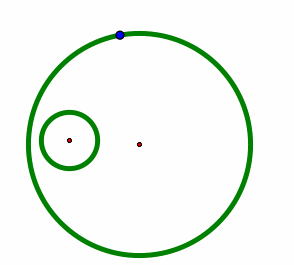
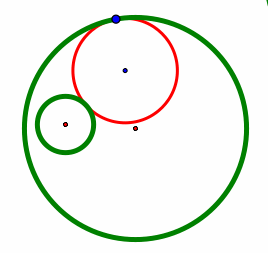
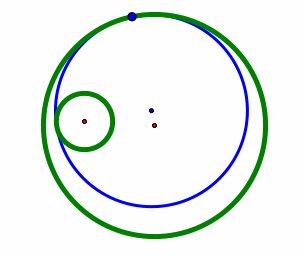
There are two different circles depicted by the red and blue circles in the last two images above. We will need both of them. So the construction should show both of them. Usually the completed construction puts both of the constructed circles on the same image.

 

 

 

We also want to explore these two tangent circles (red and blue) when the two given circles (green) are intersecting.

  

And, we want to explore the case where the two given circles (green) are completely separate or, disjoint. Here the red circle passes between the two given circles. It is internally tangent. The blue circle is externally tangent; it encircles both the given circles.

The Geometer's Sketchpad allows investigation, demonstration, and exploration. It is a tool for helping develop statements to be proved and the construction of new relationships. The set of circles tangent to two given circles is a very rich problem environment. GSP helps to visualize and demonstrate; it is a means to pose a considerable array of related problems and investigations.

Open a Java GSP to explore these tangent circles.

Click HERE if you need guidance on constructing the tangent circles.

 

Write up # 7:

Prepare a retrospective summary on your experience with this assignment. The summary might take a mathematical bent, stressing the underlying theorems and relationships. It might take a pedagogical bent, stressing the exploration and discovery. It might take a "here is something interesting I found" bent. Or . . . be creative . . .

 

8. Given a line and a circle with center K. Take an arbitrary point P on the circle. Construct two circles tangent to the given circle at P and tangent to the line.

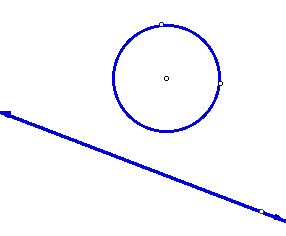
This case of the line and a circle might be considered the limiting case of the two disjoint circles. The line is in some sense a circle with an infinite radius.

 

I begin with placing point P on circle A.

 

Next I construct a line through AP and a perpindicular line to line AP to create the tangent line at point P.

 

The perpindicular line to line segment AP crosses the given line segment CD at point E (and if it doesn't, I can extend line segment CD so that it does or move point p). Now, I know I need two circles that are tangent at points P and somewhere on line segment CD. Thus, I know two tangents that the circles need to fit against, the red line and the line segment CD. Therefore, I will place one circle to the left of segment PE and the other to the right WLOG.

 

This means that the circle to the left of PE is tangent to CE, so somewhere along CE and PE lie perpindicular lines that intersect to form the center of the circle. I know that the distance from the center to the intersections of CE and PE are going to be equal distance by properties of radii. Thus, I will need to form an angle bisector line, m, of angle CEP to determine an equal distance line.

 

 

Line m crosses line AP at point I. This is the center of the circle to the left of PE and this point is equidistant from lines PE and FE by properties of angle bisector.

 

 

I can perform the same procedure to create the circle to the right by creating an angle bisector of angle PED labeled n.

 

 

Line n intersectiong line AP at point J. This is the center of the second circle where JP is the radius.

 

 

 

Here is the final construction:

 

 

In order to explore, I have reconstructed this construction so that all intersections with CD or dependencies on the line segment are dependent upon the extended line of CD.

 

Here is the updated construction:

 

Here is the clean version:

 

 

I am curious as to what happens to the circles as P is animated. I have created loci for the centers of the circles, I and J.

 

 

To see this animation for yourself, here is the GSP file for this construction.

 

It appears that the centers of the circles as P moves create parabolas where their vertices are on the line that is perpindicular to line s that passes trough point A. The loci also show that the circles disappear depending on the position of P. It looks as if this happens when PF is parallel to s as this makes sense since given two parallel lines, only one circle will be tangent to both lines.