

Kristin Ottofy
Final Assignment
A. Bouncing Barney. Your challenge is to prepare a write-up on Bouncing Barney, exploring the underlying mathematics ideas and conjectures.
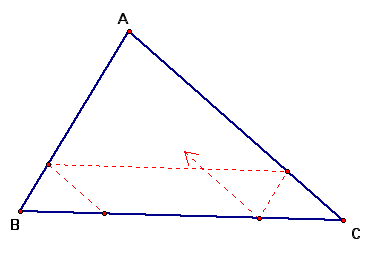
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.
I assume some GSP sketches and explorations will be useful as well as proofs of the conjectures. A highly regarded write-up will examine the extensions and interpretations of this exploration. For example,
Will Barney always return to his starting point?
If so, will Barney always travel the same distance?
Does the path create a pattern of similar triangles?
Where might his starting point be so that the path would create congruent triangles?
What if Barney started at a point inside the triangle?
Anything special about the path if he starts at the centroid? the thiocyanate?
Extend the sides of the triangle and let Barney begin his journey from a point outside the triangle. His path is slightly redefined -- rather than "bouncing" when he comes to a wall, he crosses the wall to change direction and continues to travel a path parallel to a side of the triangle. Construct a GSP image and explore.
The problem is rather open-ended. Don't give up on it too early.
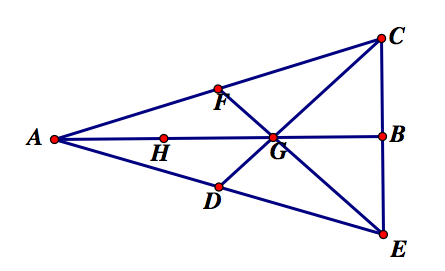
Here is a sketch of Barney's path. He begins at the blue dot and travels along line segment ED.
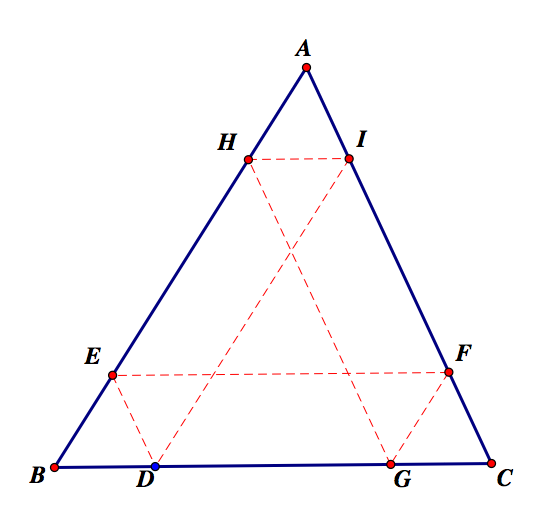
I have added some labels to the points and angle measurements using properties of parallel lines:
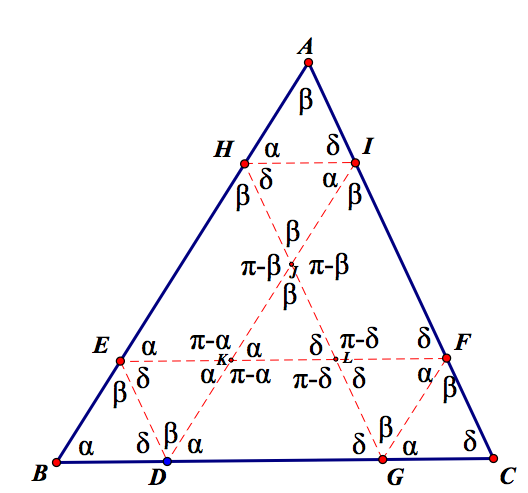
Notice, I have created 7 similar triangles. To show that Barney will return to his starting point, we can prove that triangles BED, KDE, FGL, GFC, HAI, and IJH are congruent. Looking at triangle GCF and LFG, we see that they share a common side, GF. Thus, by Triangle Congruence theorem Angle-Side-Angle, the triangles are congruent. By properties of parallelograms (or parallel lines being cut by a two parallel transversals), we can show that line segments ED, LG, FC, AI and HJ are congruent. Furthermore, line segments BD, EK, GC, LF, and HI are congruent and line segments BE, KD, FG, IJ, and AH are congruent. So, Barney will travel back to his starting point.
His total distance will be ED + EF + FG + GH + HI + ID. This is equivalent to ED + EK + KL + LF + FG + GL + LJ + JH + HI + IJ + JK + KD. Note: Because opposite sides of parallelograms are congruent, EK + KL = DG, GL + LJ = FI, and IJ + JK = HE. Substituting in those values gives: EK + DG + LF + FG + FI + JH + HI + HE + KD. Substituting in congruent line segments gives: FC + DG + GC + EB + FI + AI + BD + HE + AH. Rearranging gives: AH + HE + EB + BD + DG + GC + CF + FI + IA = AB + BC + CA. Thus, Barney will travel the perimeter of the triangle ABC.
Here is a GSP file of Bouncing Barney's travels
The graph below shows what would happen if Barney started outside triangle ABC and traveled parallel to AC first:
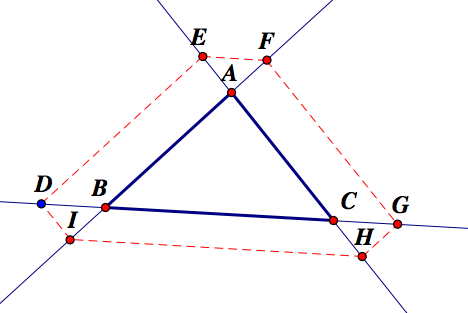
Here is the GSP file that goes with this graph.
Here are the angle congruencies:
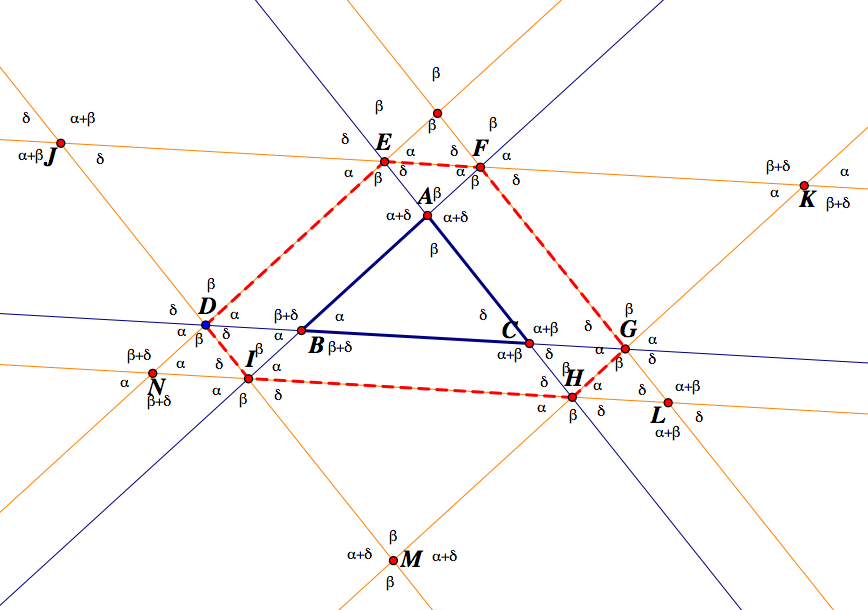
As before, we can show similar triangles and use similar calculations to show that Barney will end up in the same place using D as the starting point (blue dot) and traveling parallel to AB rather than AC first.
B. Complete a Write-up on your Web Page for one additional investigation, chosen from Assignment 0 through Assignment 12. Clearly it should be an investigation other than one you have written up before. This should be individual work.
1.1 -- Use the centroid of a triangle to develop and prove a procedure for trisecting a line segment.
As proved in Assignment 4, the centroid of a triangle crosses each median 2/3rds of the way down. Here is a graph of a centroid:
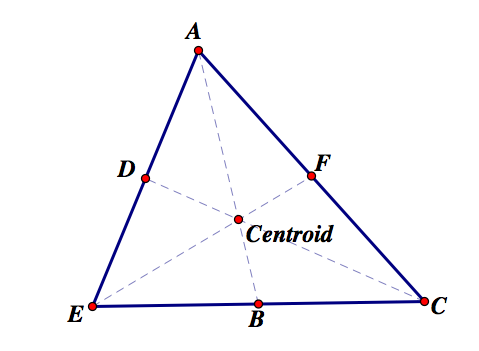
Then, if I bisect the line segment from the centroid to vertex A, I will trisect line segment AB.
Given line segment AB:
![]()
This can be the median of the triangle AEC as above.
Here I have constructed perpendicular line at point B and arbitrarily picked a point C along that line to be one vertex of the triangle. I picked a point E to be the same distance as the length of line segment BC.
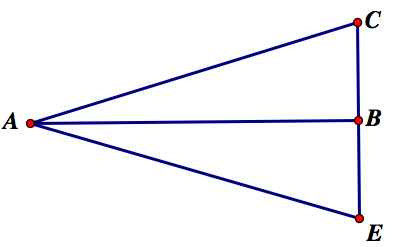
Now, AB is not only a median but also an altitude.
Here I have constructed the centroid, point G.
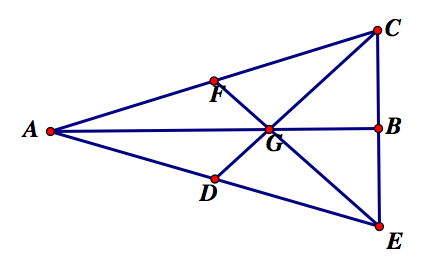
Finally, I have bisected line segment AG:
Here is the GSP file for trisecting a line segment given that it is a median of a triangle.
Note: the tool constructs line segment CB congruent to line segment AB for clarity.