

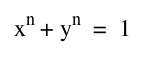
First, we will look at the graphs of the the first four equations.
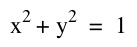
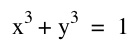
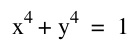
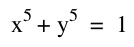
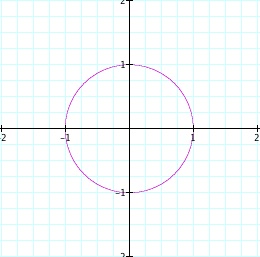
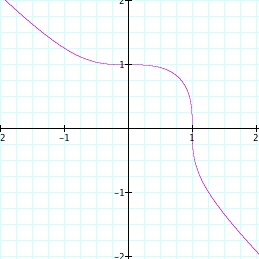
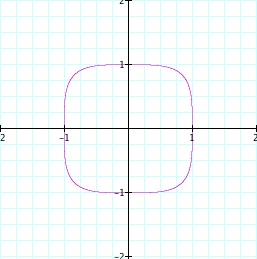
For the first equation, we see it is a circle of radius 1 centered at the origin. This was expected since it is the standard equation of a circle.
For the second equation, we observe a unique curve. The two tails of the curve act asymptotically to the line y=-x. However, there is a unique lump occurring mainly in the first quadrant. The curve intercepts the y-axis at (0,1) and also intercepts the x-axis at (1,0). It makes sense that there are no points in Quadrant III since if both x and y are negative and then squared, the result will only be a negative number. Therefore, the left hand side of the equation would always be negative and would never equal the right hand side, 1.
The third equation is similar to the first equation in that the graph contains points in all quadrants and is round in a way. It looks like it was originally a circle but was stretched outward, towards the shape of a square. However, the x- and y- intercepts are the same as in the first graph.
The fourth graph is again similar to the second graph. There seems to be a pattern starting. The intercepts are the same as the second graph and this graph has a lump in it as well. There difference here seems to be that the turns in the graph are sharper.
The commonality between these four graphs is that the intercepts remain constant. It also appears that the corners of the even degree graphs are approaching (1,1), (-1,1), (-1,-1), and (1,-1) and that the corners of the odd degree graphs are approaching (1,1), (-1,1), and (1,-1).
I believe these patterns will continue for degree 24 and 25. Since 24 is an even integer, I think that the 24th degree equation will continue expanding outwards to look more like a square. The corners should be much sharper and much closer to (1,1), (-1,1), (-1,-1), and (1,-1). Then, since 25 is an odd integer, I think that this graph will look similar to the 3rd and 5th degree equations we have already observed. Again, I think that the large majority of the graph will appear linear and will closely follow y=-x. However, for the lump in the graph around the origin, I that the turn will be sharpers and less rounded. I think that the intercepts will remain the same and the lump will have a corner that is closer to (1,1) than it was in previous odd degree graphs.
Let's look at the graphs.
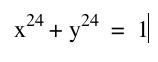
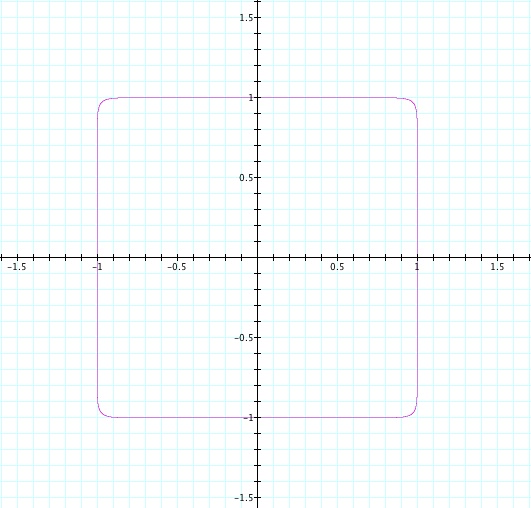
I was interested by this discovery so I wanted to keep exploring.
The next change I made was looking at negative exponents. I again found another distinction between even and odd negative integers. When n<0 and n is even, the graph consists of four different curves with each curve nearing (1,1), (-1,1), (-1,-1), and (1,-1) at its corner. Similar to the positive degrees, as n gets increasingly large in the negative direction, the corners get sharper and sharper. Visually, the graph looks like an addition symbol.
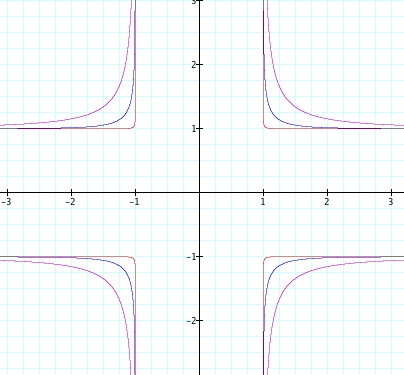
Also, if you add in an additional graph with a large positive even integer value for n, you can see that this graph fits perfectly inside the middle of the negative graph. If the n's are large enough in both directions it appears to be a graph with 4 distinct lines, y=1, y=-1, x=1, and x=-1.
Now, if n is negative but odd, the graph is completely different. There are two different components to the graph. The first, left most curve approximately follows the horizontal line y=1 until )-1,1) when it begins to follow y=-x until (1,-1) when it begins to follow the vertical line x=1. The corners between this sequence gets sharper as n increases. The second, right most curve seems to travel down x=1 until it reaches (1,1). At that point it begins to follow y=1.
The combination of the positive and negative odd values for n is quite interesting as well.
Next, I examined non-integer values for n. I looked at different fractions to se if I could come up with a pattern. I will summarize my findings below.
One conclusion that I can gather concerns the fractions with even denominators. These curves only exist in the first quadrant (excluding conditions with n=2/2 or any similar situation that reduces to whole number and therefore applies to the conditions above). Some examples of this are 5/2 and 3/4. As exponents, x^(5/2) means the square root of x raised to the 5th. The graph of this is below.
It makes sense that there are only points in the first quadrant because you cannot take an even number root of a negative number. For instance (-.75)^1/2 is undefined. So this excludes all possibilities to the left of the y-axis and below the x-axis, leaving the only possible location of the graph to be in the first quadrant since that is where both the x and y values are positive.
Moreover, the curve is concave in? when n<1 and the corner approaches the origin. When n>1 the curve is convex? and the corner approaches (1,1). Again, the assumption here is that n must be in simplest form. For instance 8/10 has an even denominator, it reduces to 4/5 and that does not.
The second conclusion that I can gather concerns the fractions with an even numerator and an odd denominator. Some examples of this are 2/3 and 4/5. The graph of these equations are continuous throughout all four quadrants. This makes sense because the outputs can be both positive and negative. Since we are taking an odd root of a value, it is defined for all real values. Then we will be raising it to an even power so we will get values in all quadrants. The graph intercepts at (1,1), (-1,1), (-1,-1), and (1,-1). The graph between these intercepts depends on the value of n.
When n<1, the graph between the intercepts caves inwards.
When n>1, the graph between the intercepts curves outward. Just as in the even integer graphs, this graph approaches a square when n is large.
Lastly, taking the absolute value of x and y results in a gradual progression from a circle to a square for all integers both even and odd. Also, taking the absolute value of x and y with no exponent results in a diamond.