

First, I want to clarify what "angle" we are talking about. If we remove the context of the football field and just look at what we have geometrically, we have a circle that goes through the two points of the uprights of the goal post and the point of the location of the kick. The segment whose endpoints are the uprights are a chord of the circle. Further, the "angle" we have is the inscribed angle in this circle described above whose vertex is the location of the kick along the line containing the hash marks. As a reminder, the measure of the inscribed angle is half of the measure of the intercepted arc, the arc of the circle between the two points of the goalpost. So, maximizing this arc will maximize the inscribed angle.
Before I begin to explain my results, I would like to give my readers the chance to explore the models I created for both the high school and college fields. The point of the kick along the hash mark can me moved and the measure of the angle of the kick will change accordingly. Click here for the file.
By using this model that I created on GSP, I found where the maximum inscribed angles are and therefore where the optimal place to kick the field goal is. I was able to drag the point of the kick along the line of the hash marks. I used the measuring capabilities of GSP to get the measure of the inscribed angle. There is only one maximum angle in the field of play. The angle decreases as the kick moves away from this optimal location in both directions. This point occurs exactly where the circle through the goal post and the location of the kick is tangent to the line through the hash marks. Although the field dimensions are different for the high school and college game, this observation holds for both cases. Further similarities between the two games include the optimal location of the kick being inside the end zone. Moving away from this point towards midfield, will only decrease the angle of kick. This stands in opposition to what the announcers believe, showing that there is no validity in their claim that kickers can sometimes gain a "better angle" by taking a penalty and kicking from 5 yards farther away.
Using this software, I found the location of the best angled kick for both high school and college. I did this by setting up a proportion. The scale on my model is 2.26 cm to 10 yards. I found that the best kick is 6.018 yards into the end zone, starting from the border of the field. The best angle for a high school field goal is 8.142 yards into the end zone.
I wanted to extend this idea to the point after touchdown (PAT) or extra point. The rules for college and high school football require the ball to be placed on the 2 yard line for the PAT. We must add 10 yards to account for the end zone and also another 7 yards to account for the setup of the kick. So both PAT's are about 19 yard kicks. Rather than coming from the hash marks, the PAT's come from the middle of the field. I was curious to who has a kick with a better angle for the PAT: the high school or college kicker? By this question, I am wanting to compare the locations of the PAT's and see who has the better angle, given the differences in the field dimensions.
Let's review some geometry first. The inscribed angle as the vertex moves along a given circle defined by the goal posts and location of the kick remains constant. So, as long as the endpoints of the angle remain constant and the vertex of the angle moves along the circle, the measure of the inscribed angle or the angle of kick will not change. Of course, when the circle itself is changed, the angle changes. There is an animation here that will help to visually explain what I am explaining.
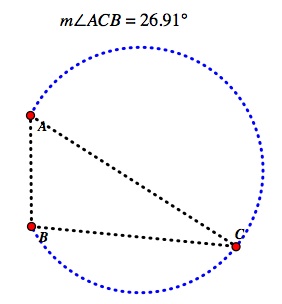
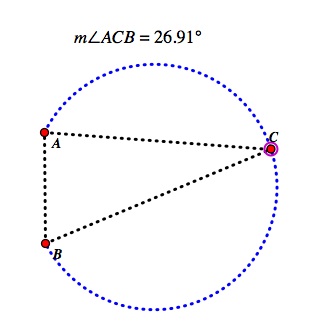
So, as long as the kicker kicks from a location on the tangent circle, the kicker will still have the maximum angle, just from a different location. These PAT's usually come from approximately the middle of the field, so I used the exact midpoint of the field for my calculations. I used proportions and the same scale as I used earlier. If the kick occurred from a location on the tangent circle, the high school kick would come from about 7.168 yards and the college kick would come from about 2.832 yards.
We must take into account again the 7 yards between where the ball is placed and where the kick occurs. Therefore, for the ball to have been kicked from these locations with the best angle, the ball would have to be placed at about the 0 yard line for the high school game and about halfway in the end zone for the college game. However, by the rules, we know that it is placed at the 2 yard line for both. From this, we can infer that the high school kickers have a better angle for the PAT than the college kickers do.
We can also use our model, scale, and proportions again to approximate the corresponding angle for the kick from the 19 yard line. For the college game, the angle is about 20.06 degrees. And for the high school game, the angle is about 25.4 degrees.
To explore the GSP file with this exploration, click here for the college field and here for the high school field.