

Here we will consider two circles and their inner and outer tangents. With these two circles, we must consider the three different cases that are created.
1. The first case is when one circle is entirely inside the other circle.
2. The second case is when one circle is completely separate from the other circle (the circles are disjoint).
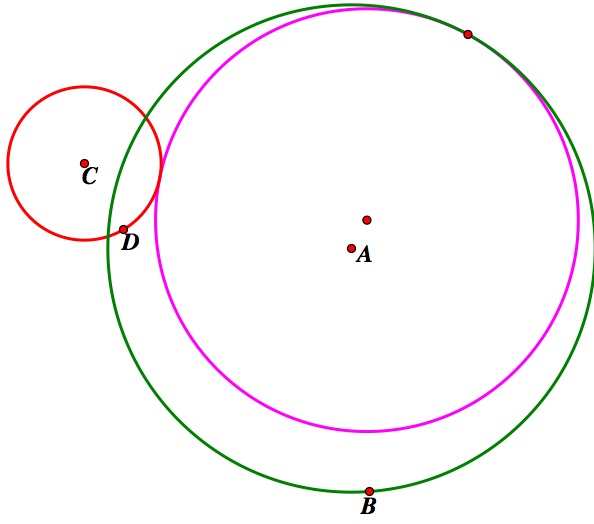
3. The third case is when one circle intersects the other circle.
In each of these cases, we can find two tangent circles to the existing circles. One of these tangent circles will be an inner tangent and the other will be and outer tangent. Both of these tangents will be common tangents, meaning that they are tangent to both of the circles.
First, I will provide pictures of each of the three cases, including the construction with just the inner tangent, just the outer tangent, and both the inner and outer tangents. The two given circles are shown in green and red. The tangent circles are both purple.
Case 1:
Inner Tangent Outer Tangent Inner and Outer Tangent
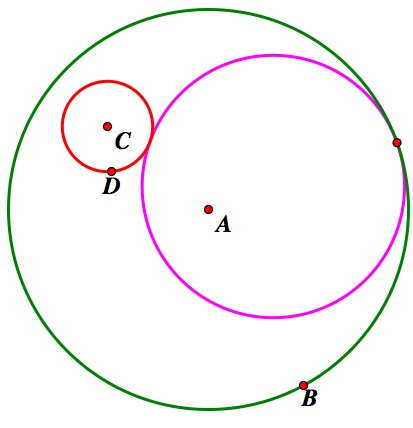
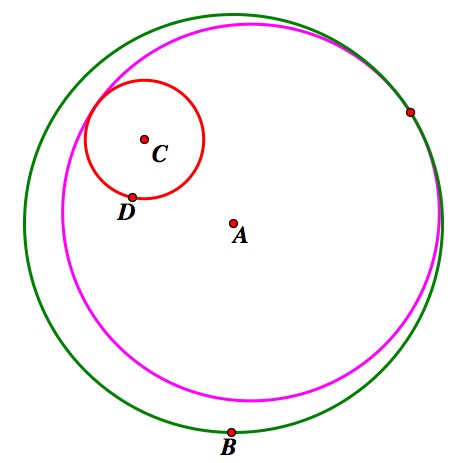
Case 2:
Inner Tangent Outer Tangent Inner and Outer Tangent
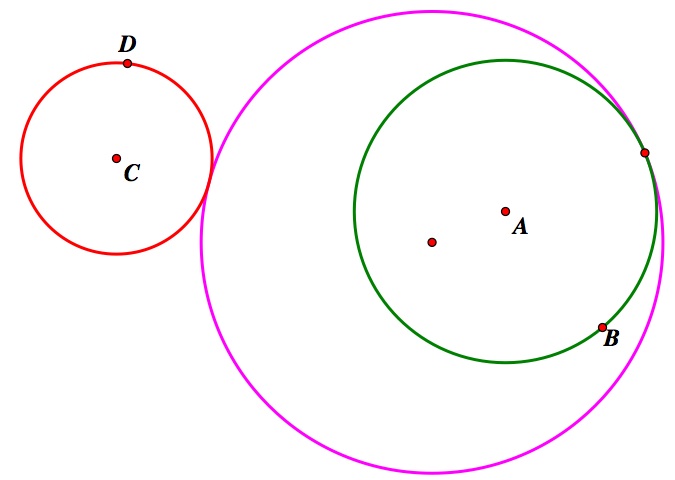
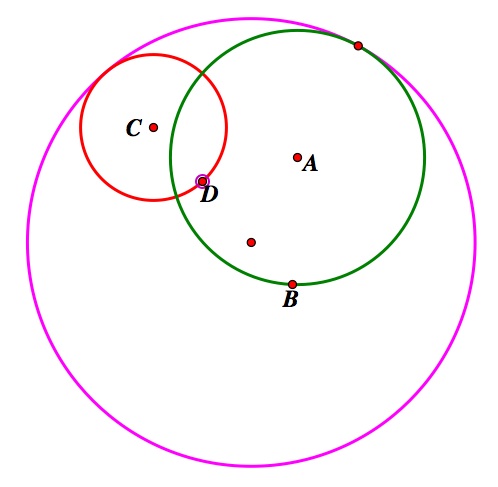
Case 3:
Inner Tangent Outer Tangent Inner and Outer Tangent

HERE is a tool to use or GSP file to explore.
Now, I will go through how I constructed these inner and outer tangents for each of these cases in GSP. I found that regardless of the location of the circles, the process of constructing each tangent, inner and outer, was the same.
To find the center of the inner tangent:
1. Construct a line through the center of the original (green) circle and the point of tangency.
2. Create a circle centered at the point of tangency with the same radius of the second (red) circle.
3. Create a segment from the center of the second (red) circle to the intersection of the copied circle centered at the point of tangency outside the original (green) circle with the line through the center of the original (green) circle and the point of tangency.
4. Find the midpoint of this segment.
5. Construct a perpendicular line of the segment at the midpoint.
6. Mark the intersection of the perpendicular line with the line through the center of the original (green) triangle and the point of tangency. This is the center of the inner tangent to the two circle
7. Construct the circle centered at that point found in part 6 with the radius equal to the distance from that center to the point of tangency.
To find the center of the outer tangent:
1. Construct a line through the center of the original (green) circle and the point of tangency.
2. Create a circle centered at the point of tangency with the same radius of the second (red) circle.
3. Create a segment from the center of the second (red) circle to the intersection of the copied circle centered at the point of tangency inside the original (green) circle with the line through the center of the original (green) circle and the point of tangency.
4. Find the midpoint of this segment.
5. Construct a perpendicular line of the segment at the midpoint.
6. Mark the intersection of the perpendicular line with the line through the center of the original (green) triangle and the point of tangency. This is the center of the inner tangent to the two circle
7. Construct the circle centered at that point found in part 6 with the radius equal to the distance from that center to the point of tangency.
Investigations with ellipses (Click to open a GSP file with the exploration below. Feel free to change the sizes of the red and green circles. The information will hold true for any size circle as long as one circle is still contained in the other. For future exploration, examine what happens when the circles intersect, are tangent, or are separate.)
I begin with two circles, one entirely inside the other. For GSP, I had a red circle contained within a green circle. Then, I added in the inner and outer tangents, showing in purple. Then, I traced the centers of these inner and outer tangent circles as the point of tangency was moved along the circumference of the larger, outside, green circle. The locus of the center of the inner tangent is shown in light blue. The locus of the center of the outer tangent is shown in orange.
But how do I know that these orange and light blue curves are ellipses?? Let us just consider the inner tangent as a similar argument can be applied to the outer tangent.
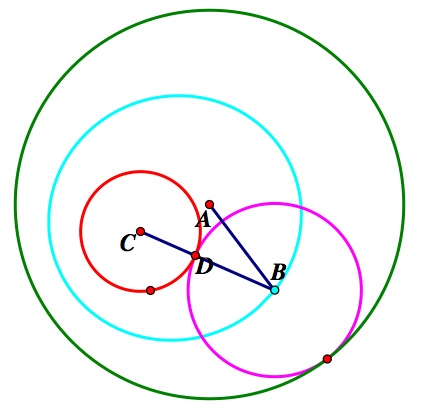
The claim is that the light blue curve is an ellipse. This can be proved because the two lines in blue, AB and BC, are a fixed distance as the tangent point moves around the circle. We know the distance is fixed because the segments are composed of the radius of the large green circle and the radius of the red small circle. AB + BD is the radius of the large green circle. DC is the radius of the small red circle. Therefore, although AB and BC vary as the tangent point moves around the circle, their sum remains constant since the circles do not change in size. So, we have shown that the blue curve, the locus of the center of the inner tangent as the point of tangency moves along the green circle is indeed an ellipse.