Here is the GSP file with a script tool for exploring and creating pedal triangles.
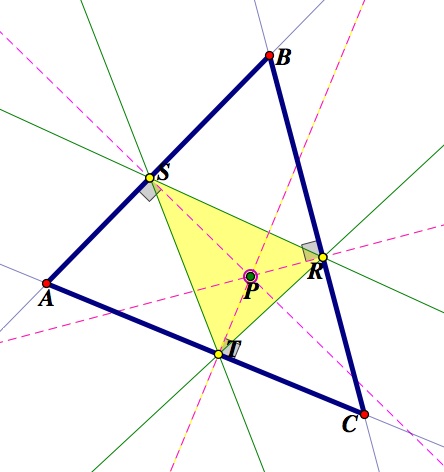
First, what is a pedal triangle??
I was going to focus my investigations on the loci of the midpoints of the sides of the pedal triangle as the pedal point, p, travels around a specified circular path. These paths were the circumcircle of the original triangle and the circle whose center is the circumcenter of the original triangle but the radius is larger than the circumcircle's (is the circle extends beyond the vertices of the triangle). When the pedal point is on the circumcircle, the triangle is a line (for further investigation or for curious minds, this is called the Simpson line). However, during the investigation of the second path, I picked up on something. I speculated that the area of the pedal triangles as p moved around the circle remained constant. This was easily confirmed with the help of GSP. I found this intriguing and decided to alter the path of my investigation. I wondered if this held for all pedal triangles whose pedal point traveled along any circle. Again, using the measuring tool of GSP, I found this to be incorrect. I was able to watch the areas of the pedal triangles change as the pedal point was animated and traveled around the incircle. I tried another example with a circle with a random center and radius, and yet again the area changed with the position of the pedal point. When I returned to my circle centered at the circumcenter with a larger radius than the circumcircle, I noticed that I could change the radius and the area still remained constant. It did not matter if the radius was bigger or smaller than the radius of the circumcircle as long as the center of the circle was the circumcenter.
So, basically, as long as the circular path that the pedal point travels along is concentric to the circumcircle, the area of the pedal triangle created will be constant. Certainly, the pedal triangle must remain on the same circle for the area to remain constant. If the pedal triangle moves to a different circle that is concentric to the circumcircle, then the area will change. However, as the pedal point moves along that circle, the area will yet again remain the same.
Before I do any more exploration, I have provided the GSP files for three different cases for the reader to explore as they wish.
Here is a GSP file for the circumcircle.
Here is a GSP file for the circle centered at the circumcenter. Feel free to change the radius.
Here is a GSP file for a circle whose center was randomly placed in the plane. Feel free to change the radius and/or the center of the circle.
But why is the area constant? And why does it hold only for circle that are concentric to the circumcircle?
For help, I turned to the internet. I found assistance in Geometry by Its History by Alexander Ostermann and Gerhard Vanner. The formula for the area of the pedal triangle
is given. That formula is
.
A' is the area of the pedal triangle.
A is the area of ABC, the original triangle.
R is the radius of the circumcircle.
d is the distance from the pedal point to the circumcenter (PO in the diagram)
This is a GSP file of the image at right. I have measured the areas of the triangles and the pedal point moves along circles that are concentric to the circumcircle.
So, let's revisit the question of why the area of the pedal triangles are constant if the pedal point moves along a circle which is concentric to the circumcircle. We can use the formula above for the area of the pedal triangle to see why this is true.
Again, our formula is
A, the area of ABC, does not change.
R, the radius of the circumcircle, does not change.
And d, the distance from the pedal point to the circumcenter, does not change as long as the pedal point remains on the same circle. This is because this distance is a radius of that circle. The circumcenter is the center of all the circles since the circles are concentric to the circumcircle. Then, the pedal point is on the circumference. Therefore, that distance is a radius of the circle and does not change as P moves along the circle.
We just showed that none of the variables in the formula for the area of the pedal triangle change as the pedal point P moves along the circumference of a circle. Thus, it makes sense that the area of the pedal triangle does not change as P moves.
From this formula, we can also make sense of the result when the pedal point moves along the circumcircle. When this is the case, we get a "triangle" that is a straight line. This is referred to as the Simpson Line. The area of the "triangle" is the area of a line, which should be 0. Let's look at the area formula to see if this is the case and, if so, why it is.
So, the formula is
, as desired.
