

Alex Szatkowski
Let’s first investigate the parametric curves
When a = b
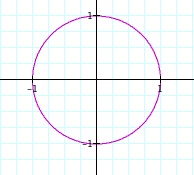
When a = b = 1 the graph is a circle centered at the origin with radius 1
When a = b = 3 the graph is a circle centered at the origin with radius 3
When a = b = -5 the graph is a circle centered at the origin with radius 5In general, when a = b = n the graph is a circle centered at the origin with a radius of |n|.
Lets look at values for which a < b
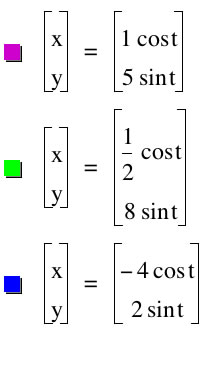
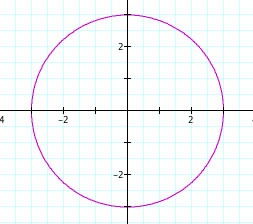
When a=1 and b=5
the graph is an ellipse with vertices at y=-5 and y=5, co-vertices at x=1 and x=-1. The y-axis is the major axis.
When a=½ and b = 8
the graph is an ellipse with vertices at y=8 and y= -8 and co-vertices at x= ½ and x=-½. The y-axis is the major axis.
When a= -4 and b= 2
the graph is an ellipse with vertices at x=-4 and x=4 and co vertices at y= -2 and y= 2. The x-axis is the major axis.*
*This is different from what we saw in the earlier two examples. I suspect it is because the absolute value of a is larger then the absolute value of b.
Therefore, when |a|<|b| the graph is an ellipse with the y-axis being the major axis and the x-axis being the minor axis. Similarly, the vertices can be found on the y-axis at (+) and (-) b and the co-vertices can be found on the x-axis and (+) and (-) a.
Lets look at values for which a > b
When a= 4 and b=2the graph is an ellipse with vertices at x= -4 and x=4 and co vertices at y=-2 and y=2. The x-axis is the major axis.
When a=6 and b= 3
the graph is an ellipse with vertices at x= -6 and x=6 and co vertices at y=-3 and y=3. The x-axis is the major axis.
When a= 5 and b= -7
the graph is an ellipse with vertices at y= -7 and y=7 and co vertices x=-5 and x=5. The y-axis is the major axis.* This is different from what we saw in the two earlier examples.
Therefore, when |a|>|b| the graph is an ellipse with the x-axis being the major axis and the y-axis being the minor axis. Similarly the vertices can be found on the x-axis at (+) and (-) a and the co-vertices can be found on the y-axis at (+) and (-) b.
Now let's investigate parametric curves of the form
When a = b
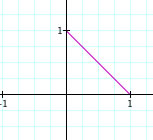
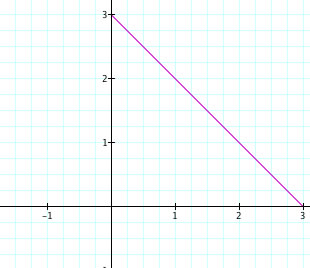
When a=b=1 we get a diagonal line from x=1 to y=1.
When a=b=3 we get a diagonal line from x=3 and y=3
When a=b=-5 we get a diagonal line from x=-5 to y=-5In general, when a=b=n the graph is a line from x=n to y=n.
Lets look at values for which a<b

When a=1 and b=5 we get a diagonal line from x=1 to y= 5
When a=1/2 and b = 8 we get a diagonal line from x= ½ to y= 8
When a= -4 and b= 2 we get a diagonal line from x=-4 to y= 2
In general when |a|<|b| we get a diagonal line from x=a to y=b. The slope of the line is greater then 1 and therefore steeper when a<b.
Lets look at values for which a>b
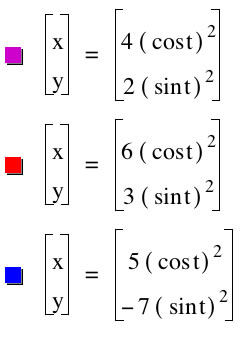
When a= 4 and b=2 we get a diagonal line from x=4 to y=2
When a=6 and b= 3 we get a diagonal line from x=6 to y=3
When a= 5 and b= -7 we get a diagonal line from x=5 to y=-7In general when |a|>|b| we get a diagonal line from x=a to y=b. The slope of the line is smaller then 1 and therefore less steep when |a|>|b|.
It is interesting to note that we do not see an enclosed shape, instead a diagonal line. I predict that with further exploration of this particular set of parametric curves we would see right triangles coming into play.
Now let's investigate parametric curves of the form
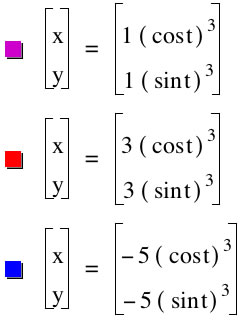
When a=b=1
we get a diamond shape with a slight curve in the sides. The points of the diamond are at x=-1,1 and y=-1,1
When a=b=3
we get we get a diamond shape with a slight curve in the sides. The points of the diamond are at x=-3,3 and y=-3,3
When a=b=-5
we get we get a diamond shape with a slight curve in the sides. The points of the diamond are at x=-5,5 and y=-5,5
In general, when a=b=n we get a diamond shape with a slight curve and the vertices at (+) and (-) n values.
Lets look at values for which a<b

When a=1 and b=5we get an elongated diamond shape with a slight curve in the sides. The points of the diamond are at x=-1,1 and y=-5,5
When a=1/2 and b = 8
we get an elongated diamond shape with a slight curve in the sides. The points of the diamond are at x=-1/2,1/2 and y=-8,8
When a= -4 and b= 2
we get an elongated diamond shape with a slight curve in the sides. The points of the diamond are at x=-4,4 and y=-2,2
In general, when a<b we get an elongated diamond shape that has vertices at x=+a,-a and y= +b and –b.
Lets look at values for which a>b
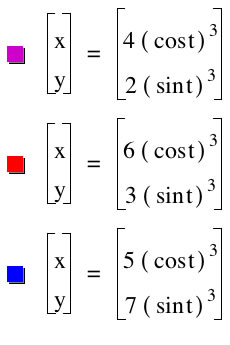
When a= 4 and b=2we get an elongated diamond shape with a slight curve in the sides. The points of the diamond are at x=-4,4 and y=-2,2
When a=6 and b= 3
we get an elongated diamond shape with a slight curve in the sides. The points of the diamond are at x=-6,6 and y=-3,3
When a= 5 and b= -7
we get an elongated diamond shape with a slight curve in the sides. The points of the diamond are at x=-5,5 and y=-7,7
In general, when a>b we get an elongated diamond shape that has vertices at x=+a,-a and y= +b and –b.
We can take a look at equations with higher powers.
For even powers 4-10
For odd powers 3-9
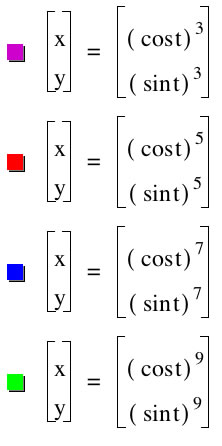
Interestingly enough we see the similar diamond with a more pronounced curved sides for odd powers, while the even powers have the same shape, however only have values in the 1st quadrant.