

Alex Szatkowski
In this investigation we will investigate ![]()
for different values of a,b and k.
To begin, lets look at when a = 0, so our equation will look more like this: ![]()
Let b vary and k stay constant at 1.
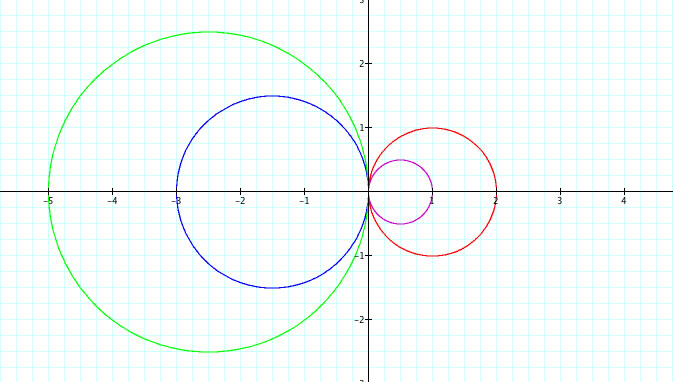
There are a few observations to make.
1. Each of these equations establishes a circle with a diameter = b, or radius ![]() .
.
2. When b < 0 the circle appears to be reflected across the y-axis.
3. All of the circles appear to be tangent at the same point.
Lets continue with a = 0 and let b and k vary
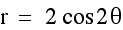
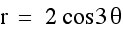
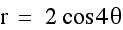
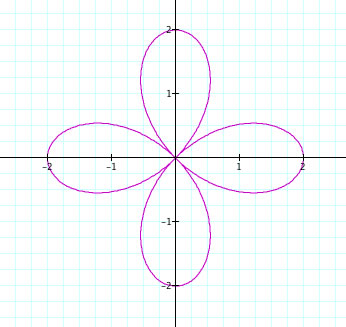
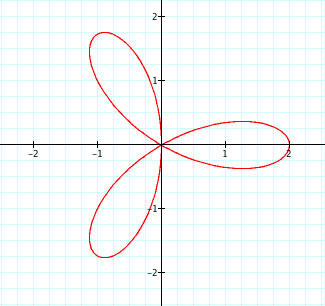
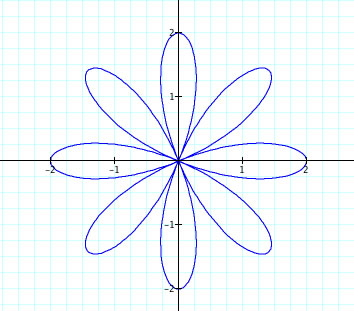
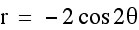
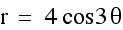
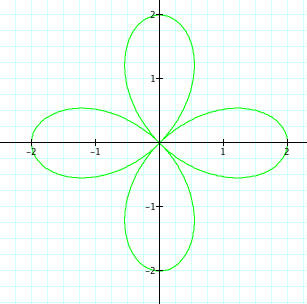
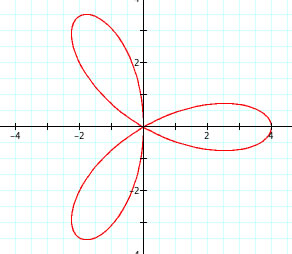
From these graphs we can make a few observations:
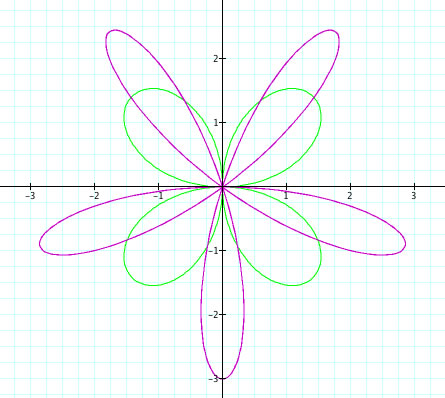
1. When a=0 and b and k vary, a Rose Polar curve is formed.
2. k determines the number of petals. When k is odd, there are k leaves. When k is even, there are
2k leaves.
3. The sign of b appears to rotate the graph 90 degrees.
4. The length of the petals is determined by the absolute value of b.
Lets now look at curves where a and b varies but k =1.
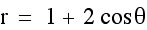
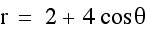
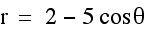
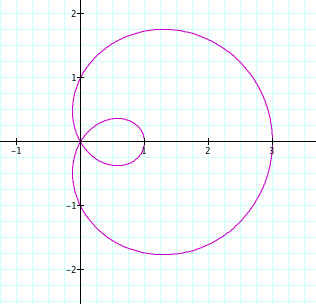
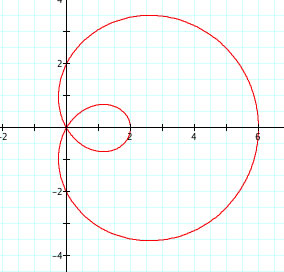
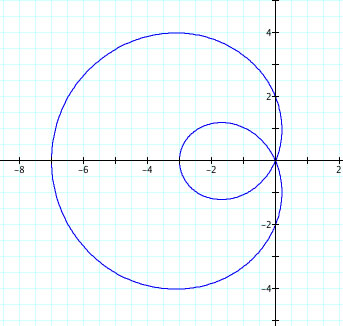
Here are some observations:
1. Parametric curves of this form form Limacon curves.
2. They all appear to pass through the origin and have an outer and inner loop.
3. |a| determines the length of the inner loop, or where it ends on the x-axis, while |b| determines the length of the outer loop, or where it ends on the x-axis.
4. When b is negative, the limacon curves is reflected over the y-axis.
Those four examples all had a positive a and a < b, lets take a look at when a is negative and when a > b.
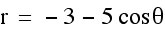
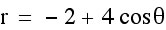
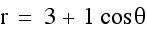
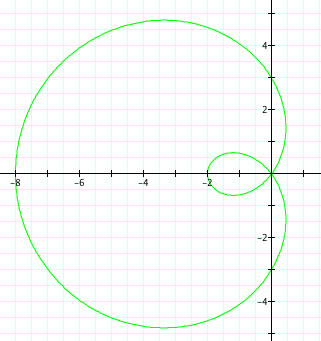
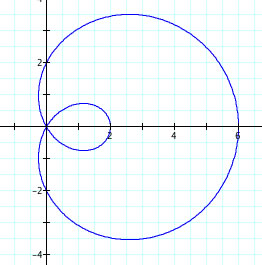
Observations:
1. The sign of "a" does not effect the graph.
2. It is very interesting that in the last two graphs, there is no loop, in fact the 3rd one looks like a circle. The third graph is called a convex limacon and the fourth graph is called a dimpled limacon. These are determined by size of the ratio b:a.
Lets look at when a=b and k = 1.
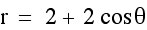
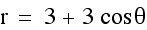
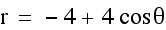
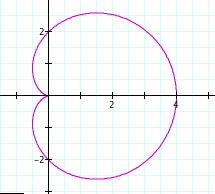
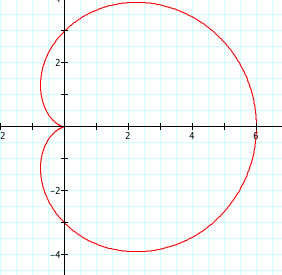
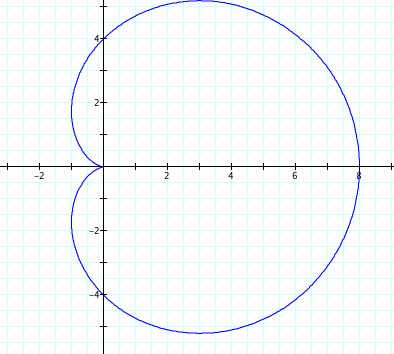
Here are some observations:
1. When |a|=|b| and k = 1 the polar equations forms a Cardiod curve.
2. When b is negative, the graph is reflected across the y-axis.
3. |a|+|b| = length of the curve from (0,0) to the edge of the curve.
These are the four out of the seven common special polar graphs.
What would happen if we replaced cosine with sine?
I predict, the orientation of the graph will change. Cosine represents the horizontal length and sine represents the vertical length in the unit circle, so I anticipate our graphs will be oriented about the y-axis.
Circle Polar Curve: Rose Polar Curve:

Limacon Polar Curve: Cardiod Polar Curve:
My predictions were correct. Changing from cosine to sine changed the orientation of our polar curves. The same results experienced from a negative b in cosine can be seen with sine just with a different orientation.