Alex Szatkowski
Lets begin by looking at the equation 
and its graph:
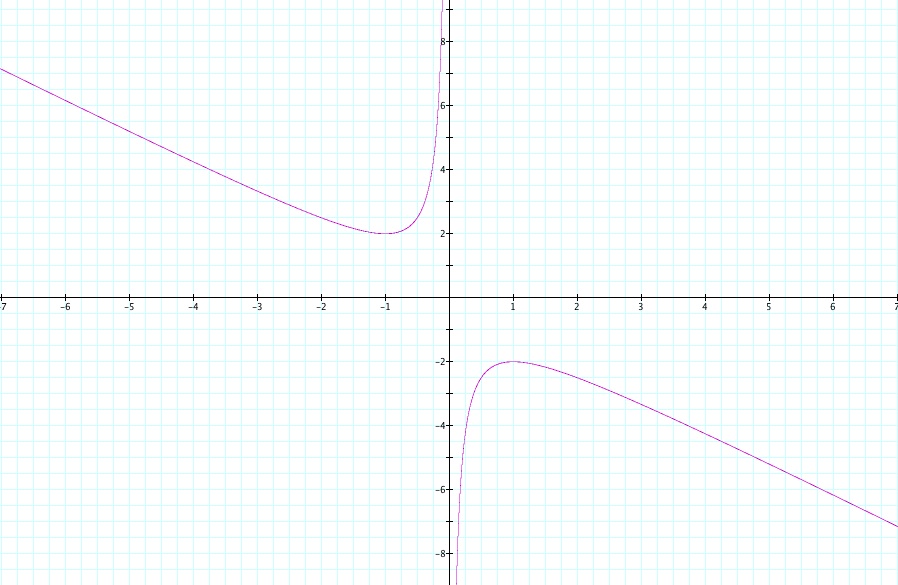
Lets investigate this equation algebraically before looking at it graphically.
First, we will solve for b.
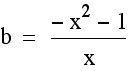
The characteristics of the graph of this function are as follows:
Domain: (-
,0) u (0,)
Range: (-,-2) u (2,)
Vertical asymptote: x = 0
Slant asymptote: y = -x
All of these characteristics are present in our graph. The graph approaches x=0 but never crosses over, similarly we see no graph between y = -2 and y = 2 which is reflected in the range. Lastly, the slant asymptote is obviouse at y = -x.
Lets look at the graph when c = 1,3,5 and 7
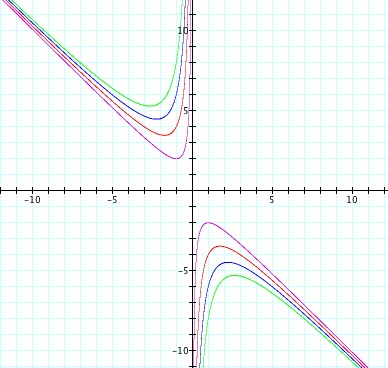
As expected, our asymptotes stay the same, however the gap in the range increases as c gets larger.
Now we will investigate the roots of these functions.
Let's take a look at the function
To solve for the roots we will use the quadratic equation and get that there are two real roots at
and
.
Both of these real numbers and therefore this function has two real roots. Let us see if this is true for all values of b.
Let b = 2, so our equation is
This can be factored to: (x+1)(x+1) = 0 so there is only one root which is real, x = -1
Take a look at the graph:
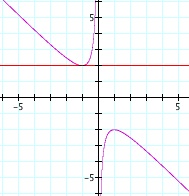
By looking at the graph of
Let b = 1, so our equation is
We must use the quadrtic equation for this one and we get the two roots to be
and
.
Both of these roots are not real because the
will result in an imagniary number. Lets see what this looks like on a graph:
In this graph we see that the graph of
In general, when
< 0 there will be no real roots. When
Lets see when c = -1 our equation will be
Let b = -5 here is our graph:
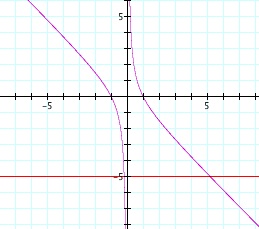
b = -5 intersects our graph twice.
If we did the algebra, our two roots will be
and
. Both of which are real numbers and one is positive and one is negative.
Lets take a look at anoter example, let b = -7
We can see that b =-7 intersects our function twice.
If we did the algebra, our two roots would be
and
. Both are real and again, one positive and one negative.
Let's take a look at a general graph for varying values of b.
By looking at this animation, for the function
we can conclude that there will always be two real roots for any value of b.
Let's look at our original function,
With this graph we can see that for some values of b there will be two real roots, two values of b for which there is one real root, and a subset of b values that will have no real roots. This mirrors what we found earlier in the exploration and in our algebra.
It appears that in general, when c < 0 there will be two roots, one positive and one negative. However, when c > 0, there can be either 0, 1, or 2 real roots depending on the value of b which helps determine the range of the function.
There are several further explorations to be done in the xb plane and in the xa and xc planes. Everything we saw in the graphs can be easily verified with algebra and vice versa.
