Alex Szatkowski
A 4 x 4 picture hangs on a wall such that its bottom edge is 2 ft above your eye level. How far back from the picture should you stand. directly in front of the picture, in order to view the picture under the maximum angle?
Looking at the picture we are provided, we can measure the angle measures. It appears that a person should stand relatively close to the picture. There may be two points where the angle is the same, but the angle will not be the maximum viewing angle. I need to find where to stand and can continue further and determine the maximum angle.
The maximum viewing angle can be found by < BDC - < ADC. Let us call < BDC angle a and < ADC angle b.
So the maximum viewing angle is a - b. Let D be the distance the person is standing from the base of the wall.
Using trigonometry, we know
therefore
.
In addition, we know
.
Since I am looking for the angles, I must solve for a and b.
So:
and
Since we established the max viewing angle is a-b:
It will help to look at the graph of a-b letting D be our variable from 0 to 10ft. Looking at the graph will give us a general idea where the max angle will be.
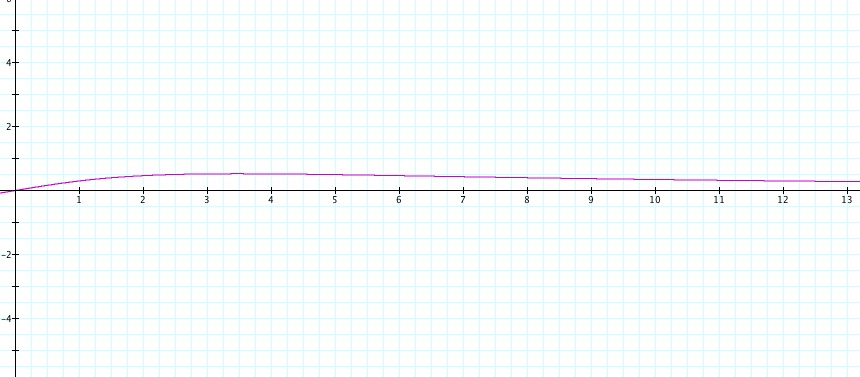
*we only need to look at 0 < x < 13 because we will not stand behind the picture, and standing too far away will take away from our view.
Looking at our graph, it appears to reach its maximum height somewhere between 2 and 4. This will help us once we perform the calculations to ensure our answer is reasonable.
In order to find our maximum viewing angle, we must use Calculus. Taking the derivative and setting it equal to zero will give us the distance someone needs to stand in order have the best viewing angle.
To refresh my memory
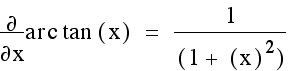I will also need to remember the chain rule.
So: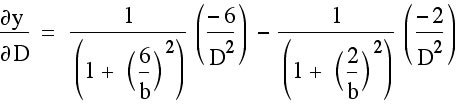 
Simplified: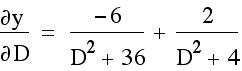 
So when the function above is equal to zero, we will have our maximum angle. Lets take a look at this graphically. (D = x)
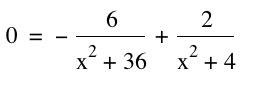
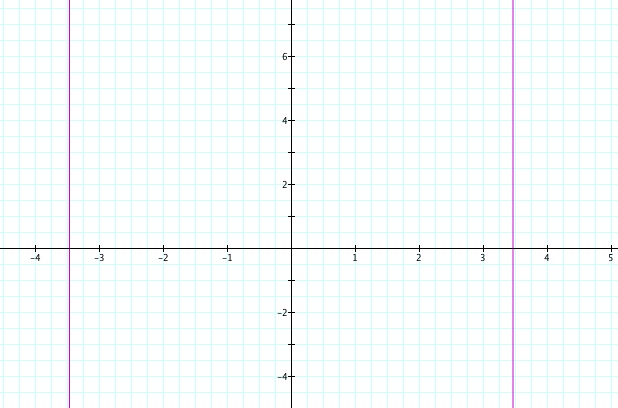
It is easy to see that there are two possible solutions. However, in this context, we will not stand behind the picture, because that would completely defeat the purpose of finding the best angle to view the picture if all we were looking at was the back of it. Therefore, the negative value is not applicable to this situation. We can estimate that the distance is going to be between 3 and 3.5.
So our estimating is getting closer...but let's find the actual distance!
We must find for what value of D is our derivative = 0.
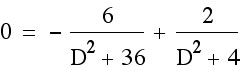
Adding the first fraction to both sides I get: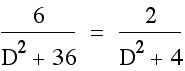 
Using cross-multiplication I get: 
I distribute "6" and "2": 
Combine like terms: 
Divide by 4 and take the square root of both sides: 
or 
Just as we concluded that a negative distance would not make sense from looking at the graph, we can determine the same here.
Therefore the distance someone should stand to see the maximum viewing angle is or approximately 3.4641 ft.
Going further, we can determing what the maximum angle actually is. To do this, I substitute .
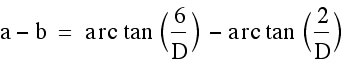
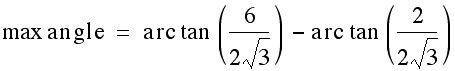
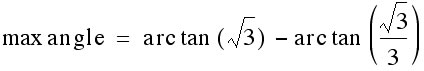
Again, we know that the angle is acute based on our picture, so we will look at these values in Quadrant 1.
and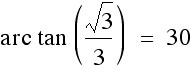 
Therefore: 60 - 30 = 30 degree angle is our maximum viewing angle.
There are many possible extensions for this problem. We could look at other accomodations for the visitors such as an addition of a bench 3 feet off the ground and how that would affect out maximum viewing angle.
