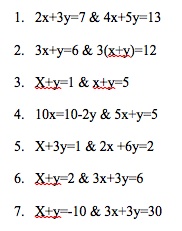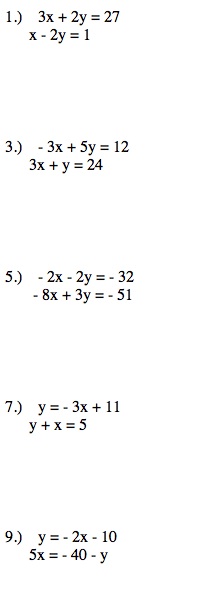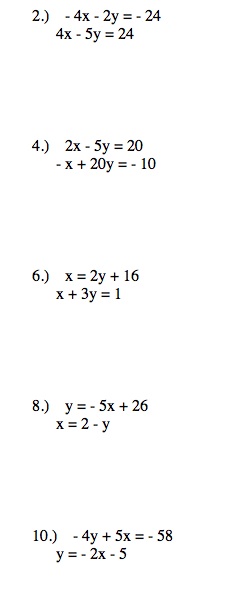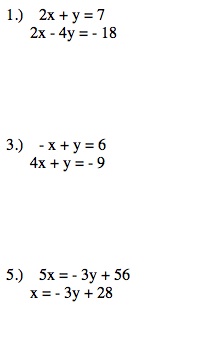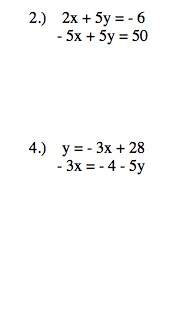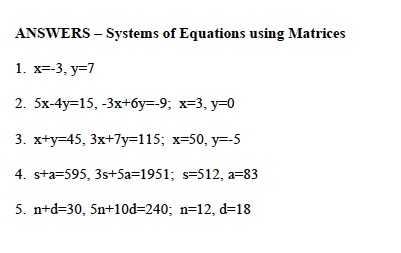Instructional Unit: Systems of Equations

Amena Warrayat

*Please maximize browser to properly view the essay*

Jump to Section:

I. Overview
II. Key Standards & Related Standards
III. Enduring Understandings
IV. Concepts & Skills to Maintain
V. Lesson Activities

Solving Systems of Equations by Graphing
Solving Systems of Equations by Substitution
Solving Systems of Equations by Elimination
Systems of Equations Game Board
Card Sort Activity & Real World Applications
Solving Systems Using Matrices


VI. Formative Assessments
VII. Summative Assessment
VIII. Alternative Assessment

I. Overview

In this unit students will:

The goal of this unit is to extend solving equations to understanding solving systems of equations, which is defined as a set of two or more linear equations that contain the same two variables. Student experiences are with numerical and graphical representations of solutions. Beginning work involves systems of equations with solutions that are ordered pairs of integers, making it easier to locate the point of intersection, simplify the computation, and hone in on finding a solution. More complex systems are investigated and solved by using graphing technology.

Contextual situations relevant to eighth graders add meaning to the solution to a system of equations. Students explore many problems for which they must write and graph pairs of equations leading to the generalization that finding one point of intersection is the single solution to the system of equations. Students connect the solution to a system of equations, by graphing, using a table, and writing an equation. Students compare equations and systems of equations, investigate using graphing calculators or graphing utilities, explain differences verbally and in writing, and use models such as equation balances.

Problems are structured so that students also experience equations that represent parallel lines and equations that are equivalent. This will help them to begin to understand the relationships between different pairs of equations. When the slope of the two lines is the same, the equations are either represent the same line (resulting in infinitely many solutions), or the equations represent parallel lines that do not have common solutions.

Solving systems in eighth grade includes estimating solutions graphically, solving using substitution, and solving using elimination. Students gain experience by developing conceptual skills using models that develop into abstract skills of formal solving of equations. Students also have to change forms of equations (from a given form to slope-intercept form) in order to compare equations.

Back to Top

II. Key Standards & Related Standards:

Mathematical standards are interwoven and should be addressed throughout the year in as many different units and activities as possible in order to emphasize the natural connections that exist among mathematical topics.


KEY STANDARDS

Analyze and solve linear equations and pairs of simultaneous linear equations.
MCC8.EE.8 Analyze and solve pairs of simultaneous linear equations.
a. Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.

b. Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6.

c. Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.

RELATED STANDARDS

Analyze and solve linear equations and pairs of simultaneous linear equations.
MCC8.EE.7 Solve linear equations in one variable.

STANDARDS FOR MATHEMATICAL PRACTICE

The Standards for Mathematical Practice describe varieties of expertise that mathematics educators at all levels should seek to develop in their students. These practices rest on important “processes and proficiencies” with longstanding importance in mathematics education. The first of these are the NCTM process standards of problem solving, reasoning and proof, communication, representation, and connections. The second are the strands of mathematical proficiency specified in the National Research Council’s report Adding It Up: adaptive reasoning, strategic competence, conceptual understanding (comprehension of mathematical concepts, operations and relations), procedural fluency (skill in carrying out procedures flexibly, accurately, efficiently and appropriately), and productive disposition (habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy).

1. Make sense of problems and persevere in solving them. In grade 8, students solve real world problems through the application of algebraic and geometric concepts. Students seek the meaning of a problem and look for efficient ways to represent and solve it. They may check their thinking by asking themselves, “What is the most efficient way to solve the problem?”, “Does this make sense?”, and “Can I solve the problem in a different way?”

2. Reason abstractly and quantitatively. In grade 8, students represent a wide variety of real world contexts through the use of real numbers and variables in mathematical expressions, equations, and inequalities. They examine patterns in data and assess the degree of linearity of functions. Students contextualize to understand the meaning of the number or variable as related to the problem and decontextualize to manipulate symbolic representations by applying properties of operations.

3. Construct viable arguments and critique the reasoning of others. In grade 8, students construct arguments using verbal or written explanations accompanied by expressions, equations, inequalities, models, and graphs, tables, and other data displays (i.e. box plots, dot plots, histograms, etc.). They further refine their mathematical communication skills through mathematical discussions in which they critically evaluate their own thinking and the thinking of other students. They pose questions like “How did you get that?”, “Why is that true?” “Does that always work?” They explain their thinking to others and respond to others’ thinking.

4. Model with mathematics. In grade 8, students model problem situations symbolically, graphically, tabularly, and contextually. Students form expressions, equations, or inequalities from real world contexts and connect symbolic and graphical representations. Students solve systems of linear equations and compare properties of functions provided in different forms. Students use scatter plots to represent data and describe associations between variables. Students need many opportunities to connect and explain the connections between the different representations. They should be able to use all of these representations as appropriate to a problem context.

5. Use appropriate tools strategically. Students consider available tools (including estimation and technology) when solving a mathematical problem and decide when certain tools might be helpful. For instance, students in grade 8 may translate a set of data given in tabular form to a graphical representation to compare it to another data set. Students might draw pictures, use applets, or write equations to show the relationships between the angles created by a transversal.

6. Attend to precision. In grade 8, students continue to refine their mathematical communication skills by using clear and precise language in their discussions with others and in their own reasoning. Students use appropriate terminology when referring to the number system, functions, geometric figures, and data displays.

7. Look for and make use of structure. Students routinely seek patterns or structures to model and solve problems. In grade 8, students apply properties to generate equivalent expressions and solve equations. Students examine patterns in tables and graphs to generate equations and describe relationships. Additionally, students experimentally verify the effects of transformations and describe them in terms of congruence and similarity.

8. Look for and express regularity in repeated reasoning. In grade 8, students use repeated reasoning to understand algorithms and make generalizations about patterns. Students use iterative processes to determine more precise rational approximations for irrational numbers. During multiple opportunities to solve and model problems, they notice that the slope of a line and rate of change are the same value. Students flexibly make connections between covariance, rates, and representations showing the relationships between quantities.

Back to Top

III. Enduring Understandings

Back to Top

IV. Concepts & Skills to Maintain

It is expected that students will have prior knowledge/experience related to the concepts and skills identified below. It may be necessary to pre-assess in order to determine if time needs to be spent on conceptual activities that help students develop a deeper understanding of these ideas

Back to Top

V. Lesson Activities

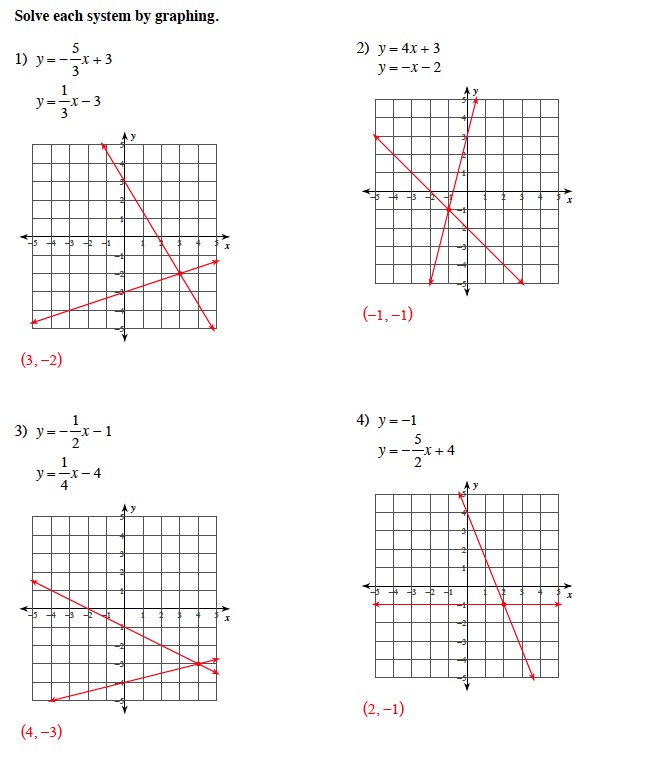
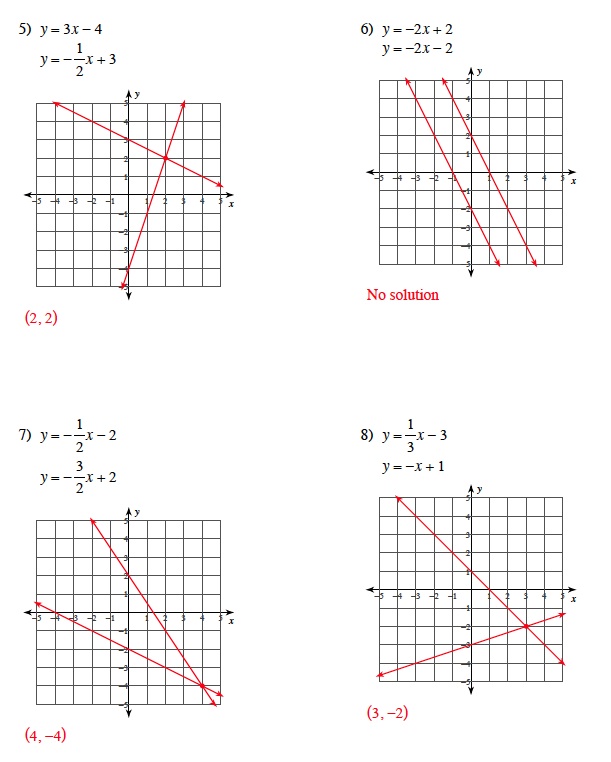
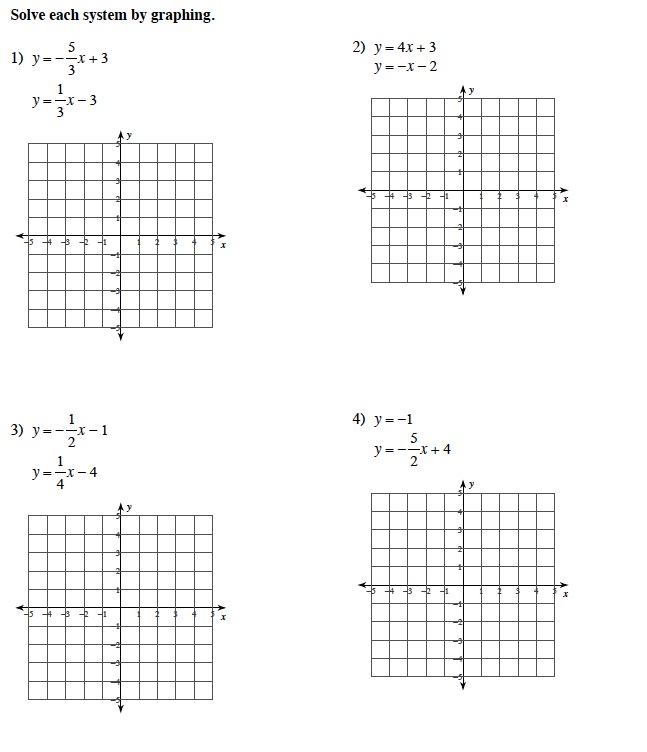
Solving Systems of Equations by Graphing

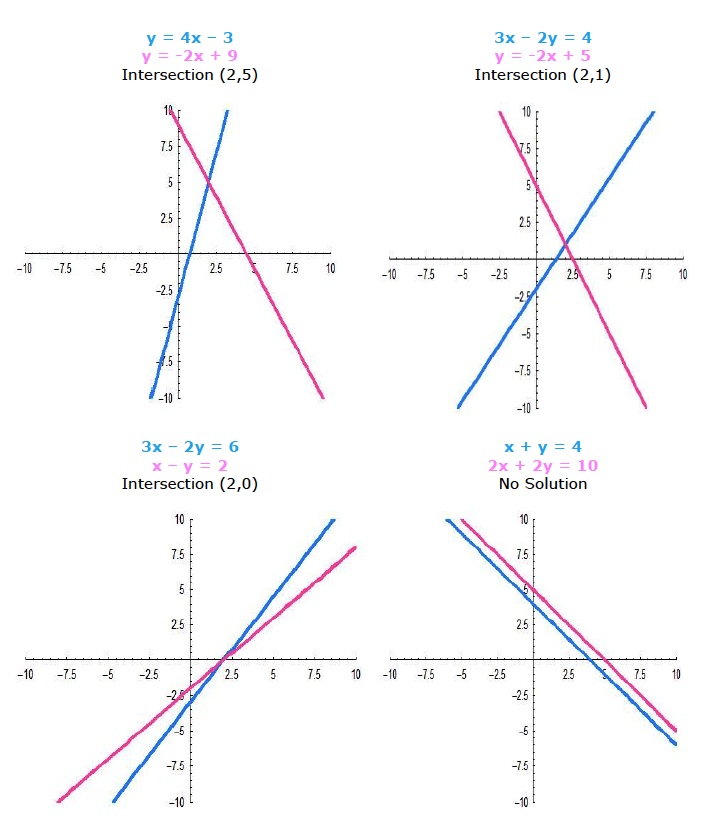
In this lesson, students will learn to graph, analyze, and solve systems of equations by using slope- intercept, standard, and point- slope forms of equations. Students will learn how to find 1 solution, no unique solution, or no solution by graphing system of equations. Emphasis will be on graphing systems of equations, with students leveraging their graphing skills as well as using GeoGebra to capture exact solutions. The primary math involved in solving systems by graphing is graphing. By graphing these linear equations, the solution needs to be common to both equations. By graphing these linear equations, students in addition will have to perform substitution to verify the solution is valid for both equations.

This two-day lesson is visually based using Powerpoint presentation, Smartboard notebook presentation, and GeoGebra with interactive kinesthetic exercises. So students will follow teacher with classroom examples- using handout of graph paper. After graphing examples in class, students will haveclassroom assignment using GeoGebra- exploring solutions of 2 linear equations manipulating slope (m) and y intercept (b) of each equation.

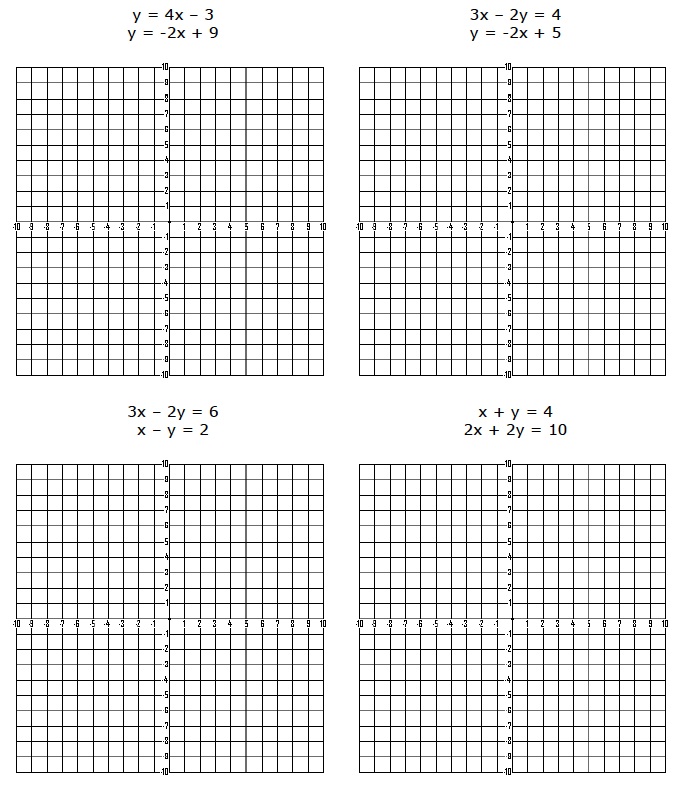
Below are some examples of systems appropriate for eighth grade students and an example of a GeoGebra assignment.

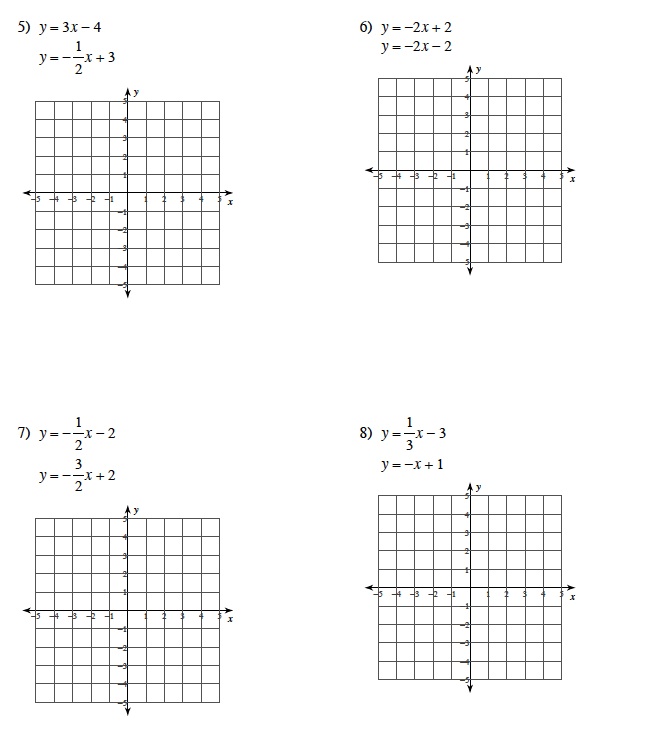
Then, students can complete a GeoGebra interactive exercise, exploring linear solutions by changing slope and y intercept values using sliders.

 

Solving Systems of Equations by Substitution

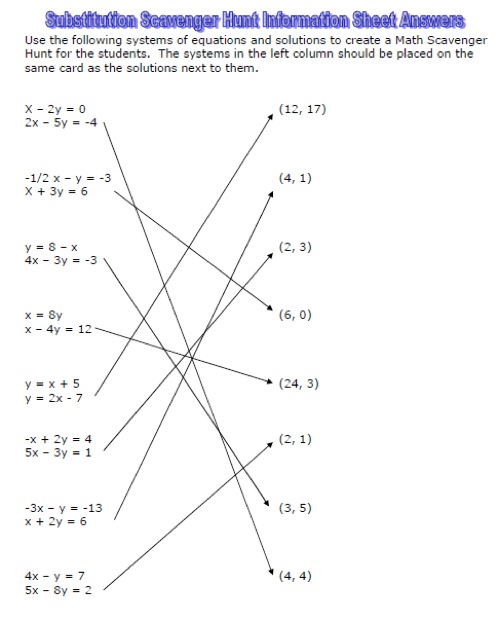
An interesting way to expose eighth grade students to solving systems of equations by the method of substitution is to have them complete practice problems by hand and using technology. Solving systems both ways can help students view technology as an excellent math resource and increase their appreciation for using technology for academic purposes. For this three-day lesson, students are introduced to the method, solve sample problems by hand, and then use graphing calculators (such as a Texas Instrument-83 or 84) to graph the systems. Afterwards, students complete a scavenger hunt of solving systems by substititution. Using the graphing calculator in this lesson will help student understand that the solution of a system of linear equations is the intersection point of the two linear functions. It also emphasizes that solving the system of equations using an algorithm such as substitution will yield the same answer as solving the system of equations by graphing. This particular concept was difficult for my current eighth grade students to understand, but using the graphing calculators in the manner described can potentially help bridge that gap.

Below are just a few examples of appropriate systems of equations for eighth grade students in additon to a sample scavenger hunt I employed in my classroom. This lesson is easily differentiable by determining the level of technology used by students and by varying the difficulty of the problems.


 

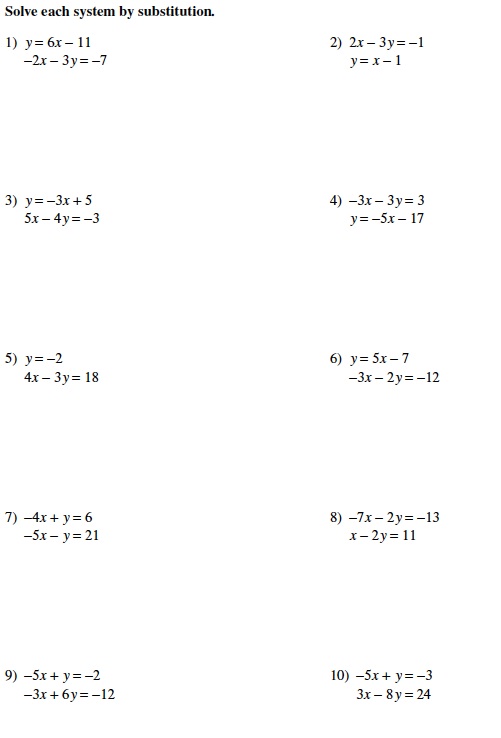
Solving Systems of Equations by Elimination

An interesting way to expose eighth grade students to solving systems of equations by the method of elimination is to have them complete practice problems by hand and using technology. Although this is similar to the previous lesson, it is extremely important to encourage students to have adequate exposure to solving systems both ways. Especially since using technology still requires students to practice the skill of converting an equation in stanard form to an equation in slope-intercept form. For this two-day lesson, below are a few examples of appropriate systems of equations for eighth grade students. This lesson is easily differentiable by determining the level of technology used by students and by varying the difficulty of the problems.

 

Systems of Equations Game Board

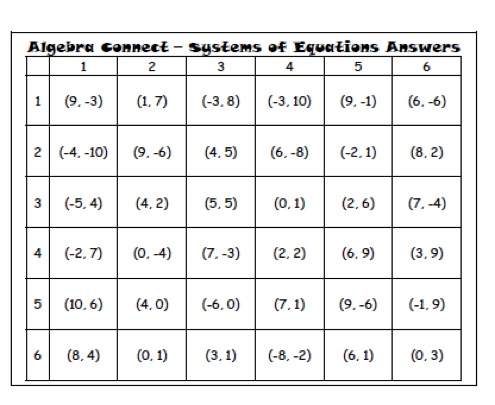
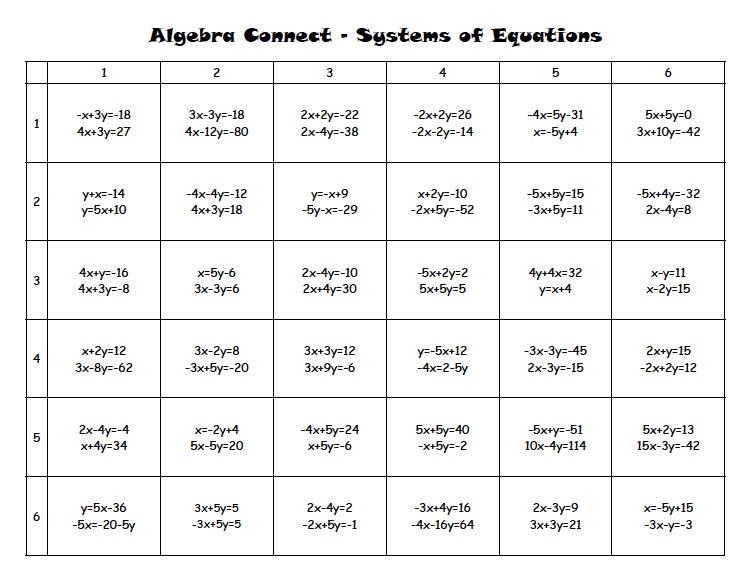
The purpose of this one-day lesson is to review solving systems by substitution and by elimination in an interactive way. Student engagement is oftentimes directly linked to the way lessons are implemented. By incorporating a game board and allowing students to solve systems in competitive pairs, it encourages students to be more focused on the task and as a result have fun while doing mathematics.

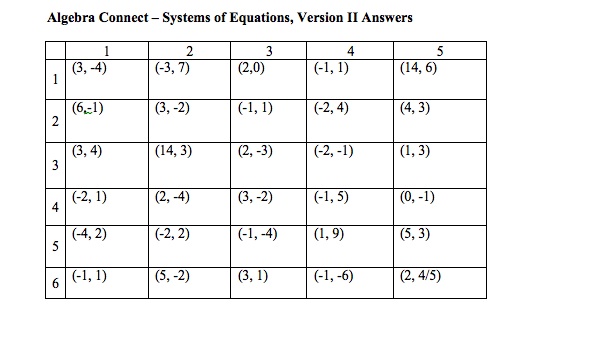
This is an example of a systems game board with the directions and answer key.

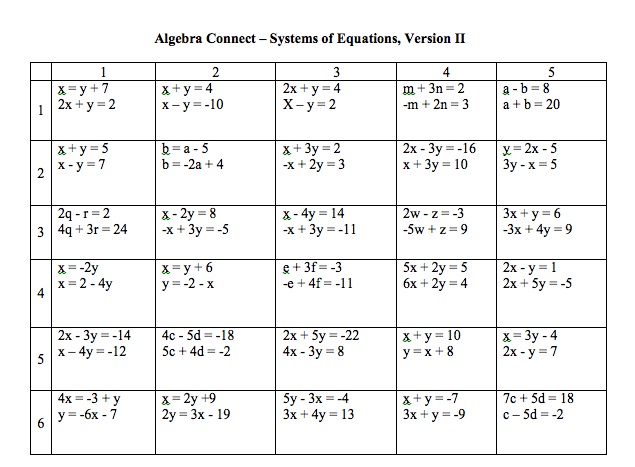
To differentiate the lesson, I created a second version of this game board, that might be more accomodating for remedial students.

Card Sort Activity & Real World Applications

To maintain high cognitive demand of our students and encourage high levels of student engagement, I propose employing this one-day lesson as a centers activity, where after an informal warm-up, the class will separate into two groups, each group to start working at a center. After approximately twenty minutes at each center, the groups will switch and work at the other center. The centers should be set up prior to the beginning of class. The first center will be where the students do a card sort in which they are given systems of equations and have to separate these systems based on the number of solutions. The three groups of solutions should be no solutions, infinite solutions, and one solution. The second center will be where students work in pairs to practice solving systems of equations of real world application word problems.

Examples of systems present at center 1:

Examples of word problems at center 2:

To differentiate the lesson, for example for remedial students, this version of word problems could be used instead:

Solving systems using Matrices

To further encourage the use of technology in the mathematics classroom, this lesson is designed to have the students practice solving systems of equations while using a graphing calculator (such as a Texas Instrument-83 or 84). To make this lesson entirely technology-based, the students can be working in the computer lab and first, be shown how a set of matrices can be used to solve systems by going to the following website. http://mathbits.com/MathBits/TISection/Precalculus/matrices.htm. This will help with the steps to inputting matrices onto a calculator and how to solve the system using matrices.

For instance, for the system:

2x + 3y = 9
5x + 4y = 5

Matrix A is 2X2
2 3
5 4
Matrix B is 2X1
9
5

Then follow these instructions:

After this introduction, students can complete several practice problems using this approach on their graphing calculators. Examples of sample problems are shown below.

 

Back to Top

VI. Formative Assessments

Throughout the unit, formative assessments should be given to the students to help identify and rectify student misconceptions. These formative assessments can be employed through tickets-out-the-door, discussion questions, pop quizzes, etc. Examples of formative assessments that can be given for each lesson is provided below.

Below is an example of formative assessment questions for solving systems by graphing. Another option that incorporates techology could be to have the students complete a GeoGebra interactive assignment that involves interpretating the graph of a system by manipulating sliders. This interactive assignment could have similar directions to the activity completed by the students in the first lesson.

Below is an example of formative assessment questions for solving systems by substitution and elimination.

Below is an example of a formative assessment for solving systems of equations in word problems, that can be administered as a ticket out the door problem.

Solve these systems:

1. The sum of the length and width of a rectangle is 19 inches. The length is one less than twice the width.
2. The perimeter of a rectangle is 48 m. The width of the rectangle is 2 more than half the length. Find the length and width.
3. Two angles are complimentary. One angle is 42 degrees more than one half the other. Find the angles.

Below is an example of a formative assessment for solving systems of equations using matrices.

 

Back to Top

VII. Summative Assessment

Version I:

Version II:

Back to Top


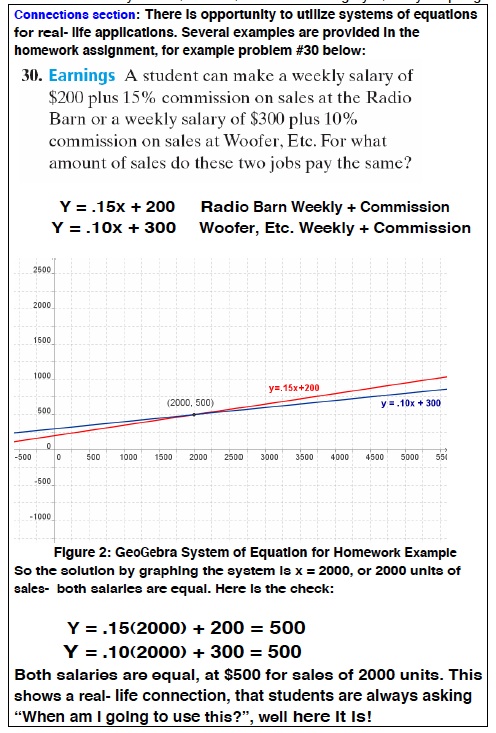
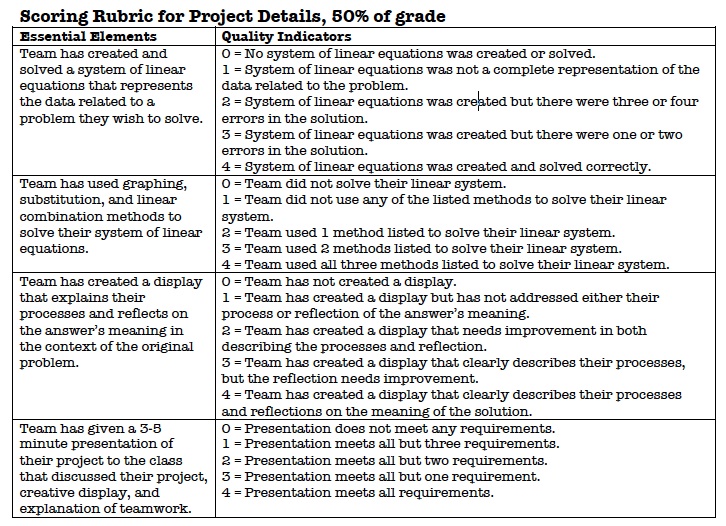
VIII. Alternative Assessment

Frequently, as a method of differentiation, alternative assessments are provided for students either as a replacement or to supplement the summative assessment for a unit. This alternative assessment is a systems of linear equations team project, which focuses on how systems are used directly in students' lives. This project could be given to students with two weeks to complete and they will have to work with a team to investigate and solve one of the situations below.

Time on this project could even be provided in class, if the instructor so chooses, but the majority of it should be completed outside of class. It should also be stressed that 50% of the project will be graded on completeness of the requirements listed in the Project
Details section using the scoring rubric below. The other 50% will be graded based on each student’s individual completion of a Team Project Processing Form, provided in class after presentations are given. This form provides each student with the opportunity to reflect on their individual contributions to the team, what they would do differently if they did this project again, and the most important thing they learned from the project. Please do not make your grade the focus of this project! The point is to learn how systems of linear equations are used in our every day lives.

Back to Top

 

Return to Amena's Homepage