*Please maximize browser to properly view the write up*
To discuss the mathematical interpretation of the parameters a, b, and c in the graph of
y = a sin(bx + c),
we individually analyze each of these parameters graphically and formally.
Manipulation of the amplitude (denoted as the constant a), period (angular frequency is denoted as the constant b), and horizontal shift, also known as phase shift (denoted as the constant c).
When a is positive:
When a is negative:
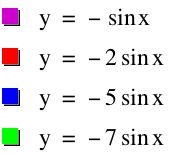
When b is positive:
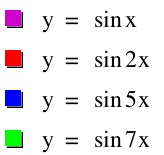
When b is negative:
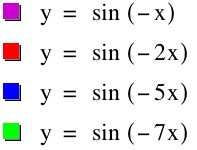
When c is positive:
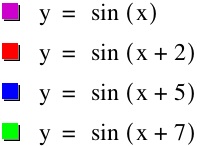
When c is negative:
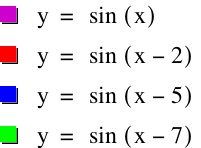
Examining the changes in the graph of y = a sin (bx + c) through animation is also insightful, as demonstrated below.
(a) Manipulation of the amplitude (denoted as the constant a)
According to this graph it is noted that at a = 0, the function is simply a constant at y = 0. As a increases from 0 to 10, we notice the amplitude increases, which indicates that the sinusodial function elongates. For negative values of the amplitude a, it is reflected across the x-axis and as the magnitude of a increases, the amplitude again increases.
The mathematical interpretation of amplitude a:
Amplitude is the peak deviation of the function from its center position. It can be thought of as the maximum and minimum values of the function.
(b) Manipulation of the period (angular frequency is denoted as the constant b).
When b is a negative value, the sinusodial function is reflected over the x-axis. As the magnitude of b increases, the period increases which indicates within a specific unit length on the x-axis, there are more copies of the sinusodial functions.
The mathematical interpretation of frequency:
Angular frequency specifies how many oscillations occur in a unit time interval, in radians per second. The change in b is a change in frequency which directly affects the period. The formula that relates period (P) to frequency (b) is:
where p is the wavelength. We note that the period and frequency are inversely related.
(c) Manipulation of the horizontal shift, also known as phase shift (denoted as the constant c).
According to the graph, the sinusoidal function translates to the left by
(as compared to the parent function sin(x)) when c is a positive value, and translates to the right by
The mathematical interpretation of phase shift:
The phase specifies where in its cycle the oscillation begins at the start time (i.e. t= 0). When the phase is nonzero, the entire waveform appears to be shifted in time by the amount
seconds. A negative value represents a delay, and a positive value represents an advance.
