

Problem ten states,
Investigate each of the following for
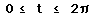
Describe each when a = b, a < b, and a > b.
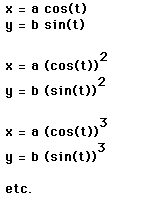
We see with a = b = 1, the graph is a circle with radius of 1.
Exploration, Part 1: a = b, a < b, and a > b.
Consider:
What will happen when the values of a and b are not equal to 1?
Case 1: a=b. For now, we explore the situation where a = b = 3.
We get a circle with a radius of 3. It seems like the radius of the circle is determined from the value of a = b. Let's look at the situation where a = b = 5 and see if the radius of the circle is 5.
The radius is 5. Our perception that the radius of the circle is determined from the value of a = b is correct.
Case2: a>b. For now, we explore the situation where a = 5 and b is an integer from the set {1, 2, 3, 4}.
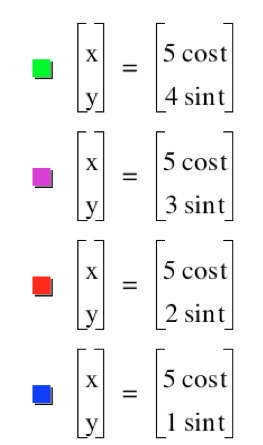
Notice that the graphs are all elipses. As the value of b decreases, the ellipse lengthens along the y-axis. Notice that since the value of a = 5, the elipse passes through x = 5 and x = -5 for all the ellipses.
Case 3: a<b. For now, we explore the situation where b = 5 and a is an integer from the set {1, 2, 3, 4}.
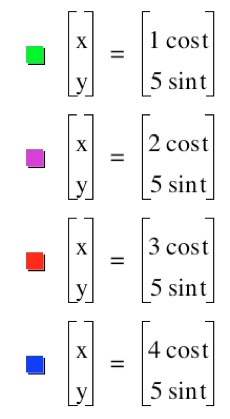
Again, every graph is an elipse, this time widening along the x-axis. As the value of a changes, the elipse intersects the x-axis at the x = a and x = -a. Notice that since the value of b = 5, the elipse passes through y = 5 and y = -5 for all the ellipses.
Exploration, Part 2: Using exponents
It will also be interesting to explore the following equations.
Consider:
We get a line segment from (1,0) to (0,1). What happens though if we change the values of a and b?
Case 1: a=b.
Notice that we get a line segment from (3,0) to (0,3). It seems as if the values of a and b affect where this segment intersects the x and y axes.
Case 2: a<b. For now, let's explore the situation where a = 1 and b = 3.
Interestingly, this line segment connects the points (3,0) and (0,1). One might conclude that the value of a is where this line segment will intersects the x-axis and the value of b is where this line segment intersects the y axis.
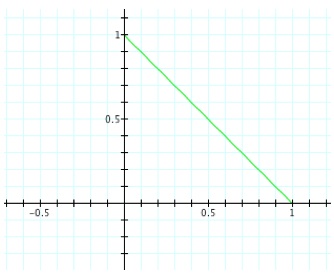
Case3: a>b. For example, let's consider a = 3 and b = 1.
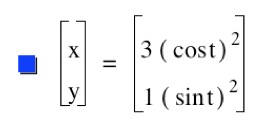
Again we conclude that the value of a is where this line segment will intersects the x-axis and the value of b is where this line segment intersects the y axis. With a=3, the line intersects the x-axis at (3,0) and with b = 1, the line intersects the y-axis at (0,1).
Let's explore this idea as the exponent increases. Consider the cube power, setting a = 1 and b = 3.
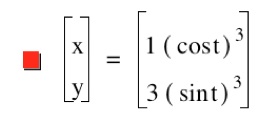
Again, our values of a and b affect where the graph crosses the axis, but now we see more than a line segment. We see a diamond shape with a slight curve. The shape connects with the x axis at our value of a and the y axis at our value of b. Is it safe to assume if we switch the values of a and b, then we will get the same diamond shape, only crossing at (3,0), (0,1), (-3,0), and (0,-1)? Notice:
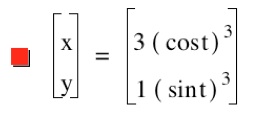
Yes, it is clear again the values of a and b affect the points at which the graph touch the x and y axis. Here we have the same shape, only the graph crosses the axises at (3,0), (0,1), (-1,0), and (0,-3).
Let's explore with even higher exponential values. First, consider when a=1 and b=3 and take our exponents to be 3 through the 7 power.
Now consider when a=3 and b=1 and take our exponents to be 3 through the 7 power.
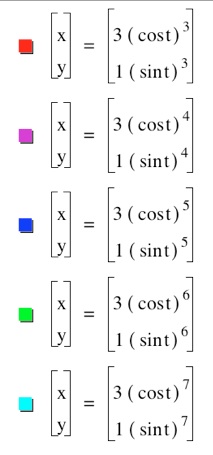
We can see as the exponent value increases, the curve is more pronounced. The graphs cross the axes based on the values of a and b. Therefore, when a>b, the graph will be elongated along the x axis and when a<b, the graph will be elongated along the y axis. Yet, if we look closely, we notice something interesting. We see that for even exponents, the graph remains in Quadrant I, while with odd powers, the graph is in all four Quadrants.
Further explorations may look into when sine and cosine are negative or positive. Also, adding and subtracting integers from each equation can lead to many further explorations.