

Final Project
Drew Wilson
Will Barney always return to his starting point?
There are three different scenerios we need to look at to decide if Barney will always return to his starting point. We need to look at the case when he starts at one of the vertices. We need to look at the case when he starts at the midpoint of side length BC and we need to look at the case when he starts at any other point on side BC.
We know that if Barney starts at one of the vertices, he has only two options. Say he starts on vertex B, then the two options he has is to walk to vertex A or walk to vertex C. When he gets to the vertex he walked to he is faced with two more options which involve the vertex he just came from and the vertex he decided not to walk to. In this sense he will be travelling along the walls the entire time and will eventually arrive at his starting point.
If Barney starts at the midpoint of BC and he travels parally to AC, then he will end up at the midpoint of BA. Now when he leaves the midpoint of BA he will travel parallel to BC and he will arrive at the midpoint of AC. Now from this point he will travel parallel to AB and he will arrive at the midpoint of BC which is where Barney started. Therefore, if Barney starts at the midpoint of BC, he will arrive at his starting point after two changes in direction.
If Barney starts at any point along side BC, then he will follow the rules in the problem by travelling parallel to AC, then when he hits side AB he travels parallel to BC, then when he hits AC he travells parallel to AB and the process repeats itself. Here is a sketchpad document that will allow you to change Barney's starting point along side BC. You can make his starting point the midpoint, a vertex or any point along the line BC. Notice that the light blue lines represent the path that Barney has walked and also notice that the dark blue dot represents the starting point of Barney. If you move Barney's starting point, you will notice that there are two light blue lines that connect to Barney's starting point. One line represents the path Barney took when he left his starting point and the other line represents the his path coming back to his starting point. This shows that no matter where Barney starts along side BC, he will always return back to his original starting point.
Will Barney always travel the same distance?
Here is a link to a GSP file that you can look at and change Barney's starting point. Notice that the colors in this picture represent the same thing as in the previous exploration. Now notice that the total distance travelled by Barney is given at the top right of the document. Move Barney's starting point along side BC and notice the change in the total distance travelled by Barney. No matter where Barney starts, his total distance will always remain the same.
Does the path create a pattern of similar triangles?
Sine Barney's path is always parallel to one of the sides of the triangles, we know that Barney is forming similar angles at each change in direction. The question is whether or not the similar angles form similar triangles. If we look at our triangle below, then we will notice that the triangles formed by Barney's path are indeed similar triangles. We can see this by thinking about the properties found by a line intersecting two parallel lines. In the case that Barney's starting point is not at the midpoint or on one of the vertex there are two parllel lines formed to each side (side BC has two parllel lines, AB has two parallel lines, and AC has two parallel lines). So we are able to see what angles are the same by our properties of a line intersecting two prallel lines. We know that each triangle formed by a line parallel to the original triangle will have the same angle. Therfore, as you can see below, Barney's path does create similar triangles. Each congruent angle is represented buy the same measure of angle sign.
Where might his starting point be so that the path would create congruent triangles?
If Barney starts at the midpoint of BC, then his path will construct 4 congruent triangles. We know that because as mentioned earlier when he started at the midpoint of BC, then the vertices of his path were the midpoints of AC and AB. Since his path was triangular because he changed direction two times and arrived back at this starting point and since each vertex is located at the midpoint of each side of the orginial triangle, he constructed the medial triangle. We know that the medial triangle divides the original triangle into 4 congruent triangles. Therefore, if Barney was to start at the midpoint of BC, then his path would create 4 congruent triangles. If you notice the figure below, congruent angles are marked by similar signs and congruent sides are marked by similar sides as well.
What if Barney started at a point inside the triangle?
If Barney started at a point inside the triangle, then there would be no change in the outcome. If we think about when Barney started walking in the original cases above, then we can think about Barney starting on the line formed from his starting point on BC to where he changes direction on AB, this line would be represented by the line DE above. Refer back to the link above when I provided you with a GSP file that allowed you to move Barney's starting point and notice the different paths he could take. If you move Barney's starting point notice that the first line formed (parallel to AC and formes vertex on AB) spans the entire inside of the triangle. If Barney's starting point is on the vertex C and you move his starting point all the way to vertex B, then you will notice that the first line mentioned before spanns the entire inside of the triangle. Now imagine that Barney started at some point along that line, then Barney will arrive at his starting point because the parallel lines do not change. Now imagine that Barney's starting point could be any point along this line. Since this line spans the entire inside of the triangle, then Barney's starting point could be at any point inside the triangle. Therefore, if Barney started inside the triangle, the outcome would still be the same the only differnce is he would change direction one more time.
Anything special about the path if he starts at the centroid? the orthocenter?
When Barney starts at the centroid, then he will arrive back at his startin point in the least total distance covered. He will make two changes in direction and he will arrive at his starting point that will form a triangle similar to the one formed when he started at the midpoint of BC. If you would like to explore this phenomena using GSP and changing the size of the triangle to change the location of the centroid you can click here. Notice that Barney's path only has two changes in direction no matter what kind of triangle you form.
When Barney starts at the orthocenter, the same occurs as when he starts along the side BC. You can manipulate the triangle to form the case when Barney started at the midpoint of BC. You can see and explore this idea by clicking here, you can click and drag the vertices of the triangle that will allow you to change the location of the orthocenter. Notice how the path of Barney changes as you change the triangle.
What if Barney starts outside the triangle?
If we extend every side of the triangle and start at a point along the line BC, then Barney will still arrive at his starting point. However, he will begin his journey going the opposite direction because now in order to be parallel to AC and intersect with AB the direction Barney will start has to be opposite of when he started on the side BC. You can explore more by clicking here, you can change the starting point, D, or you can change the size of the triangle by moving the vertices of the triangle. Notice that there are always two lines connected to point D, one line is the starting line and the other line is the line of his path as he approaches his starting point.

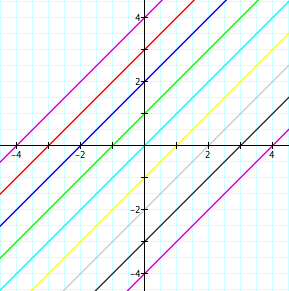
The first thing I thought about when graphing these equations was how you could use this to help students learn about linear equations and how to determine y-intercepts using linear equations. While I was thinking about this I noticed that, with this particular set of equations, not only could you help them with y-intercepts, but you could also help them with x-intercepts because since the slope of each equation is one, the x-intercept is the opposite of the y-intercept. I believe showing students all of these equations at once would be very beneficial because it would allow students to see multiple equations with only one difference in each equation, the value of b in the linear equation y=mx+b. This will help students to see how the value of b changes the graph of each function. Students will also be able to notice that the x-intercept of each equation is -b, because in order to find the x-int. you have to set y= 0 and solve for x and when you set y=0 all you have to do is subtract b from both sides to find the value of the x-int. If students view one equation at a time they may forget what the previous equation looked like and may not be able to make connections between each equation. If you graph all equations together then students can look and analyze the group of equations as a whole and be able to make inferences on how the parameter b changes the graph of the equation. An example of what these graphs would look like as a whole is provided at the right. As you can see the equation y=x+4 is represented by the top line. We can see that the y-intercept is 4 and the x-intercept is -4. We can see the same occuring for all the different equations provided. This also helps students to see that the equation where b=0 is the same as the equation y=x and thus the origin is the x and y intercepts.
The best time to use an animation to help student learning would be when you need to graph multiple graphs in order for the students to see the relationship between graphs. If the number of graphs you have to graph to show the relationship exceeds 10, then you may need to use an animation so students do not have to keep up with so many different graphs. Also, if you are working with graphs that may intersect with each other as the parameter changes, then you need to use an animation because the intersection as the parameter changes may confuse the students. Below is an animation of the function y=x+n as -4≤n≤4. Using the animation for this function may be difficult for students to pick up on the details of the graph because the graph appears to be moving diagonally when really the graph is moving vertically. This may create a misconception in student thinking because the student may think that as the value of b changes the line shifts diagonally.
There are many ways to show students how parameters change the graphs of equations. Both of these methods are very helpful in certain scenerios, and can create misconceptions in other scnerios. The decision is left with the teacher about what manipulative is used and the teacher has to be prepared to clear any misconceptions in the lesson before the misconceptions grow to the point of no return.