Assignment 1
Exploring the Sine Function
Drew Wilson
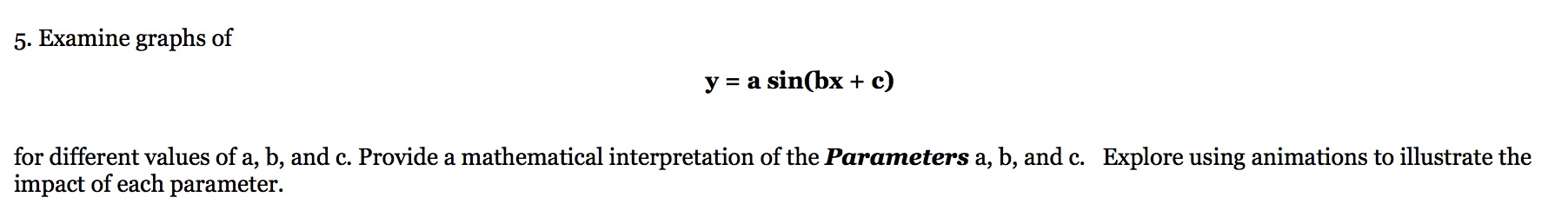
First, let's define the parameters of a, b, and c. The parameter a=amplitude which means the maximum extent of an oscillation measured from the point of equilibrium. The parameter b=period which is the amount of time it takes for one rotation to occur. The parameter c=phase shift which means the function has been translated horizontally. Now, let's analyze these different parameters.
Let us explore how the value of a affects this function. Below is an animation of how this function reacts as the value, a, changes.
As you can see above, the value of a affects the maximum and minimum y value attained by the function. If we think about this in terms of a circle, then the value, a, affects the radius of the circle. When a is equal to the value of 1, then you are dealing with the unit circle because the maximum and minimum y-value of the function is 1 and -1 with the x-axis representing the center of the circle. You would be able to see this better when the period of the function is retained to show only one period. In this function the period is fixed because the x-intercepts of the function remain the same, the only change is the distance from the x-axis. As a increases, the distance from the x-axis of the function increases by a. So, when a=15, the maximum and minimum y-values of the function occur 15 units from the x-axis in the positive and negative direction. Therefore, a, dilates the function.
Now, let us explore how the value of b affects this function. Below is an animation of the graph of this function as the value of b changes.
In this animation, the vertical red line represents one period of the sine funciton. You can see that the y-intercept never changes and the vertical line that represents one period corresponds to the y-intercept of the graph. Therefore, the value of b changes the period of the function. Since the vertical line represents one period, you can see that as the value of b increases so does the period of the function. Similarly as the value of b decreases then the period of the function decreases. We can think of this as expanding and contracting the graph while maintaining the maximum and minimum values of the graph at 1 and -1. In other words, there are horizontal asymptotes at y=1 and y=-1. In terms of a circle, the value of b affects the number of revolutions being made, so we can think about this in terms of how many times the wheel of a car turns based on how fast the car is moving. As the value of b increases, then the car is going faster because one revolution takes less time, and if the value of b decreases then the car is moving slower because it takes longer for one revolution to occur. Therefore, the value of b affects the number of revolutions over time or the period of the function.
Now, let us explore how the value of c affects this function. Below is an animation of the graph of this function as the value of c changes.
In this animation the vertical line is at x=
- c. When c is zero and a is 1, we have the original sine function that is used when dealing with the unit circle and the vertical line at x=. When the value of c changes, then the sine function is shifted horizontally to the left is c is increases and horizontally to the right if c is decreased. Let's think about this in terms of the value of sine in the unit circle. If, in this function, b=1 and c=0, then you have the original sine function. As you increase c and leave the value of b fixed at b=1, then the value of sine increases until it reaches 1, then the value decreases to -1 and increases back to 1. The first action that occurs when c increases, if you start with the original sine function, the funciton will shift left because the values of a and b are fixed at a=1 and b=1, and the angle is being increased. Similarly as c decreases, the function shifts to the right. You can see this because the vertical red line is fixed at the value of on the sine function. This line maintains this value because the equation of this line is x= - c, so if you plug - c in for x in your equation then you are left with sin(), so we know the vertical line crosses at the fixed point at . You can also see this because I set the parameters for the value of c in graphing calculator to move from -5 to 5 and when c=5 the vertical line stops at approximately -1.96 and pi - 5=-1.96. Therefore, the value of c translates the graph horizontally left and right. When thinking about the unit circle, this function maintains the size and shape of the circle, but as the value of c changes, the circle rotates about the center of the circle. As you can see in the animation, the value of for the circle is shifting horizontally based on the value of c, so the circle is spinning. As, c, increases the circle is being rotated to the right, and as, c, decreases the circle is being rotated to the left.