Assignment 2
Vertical Translations of Quadratic Equations
Drew Wilson
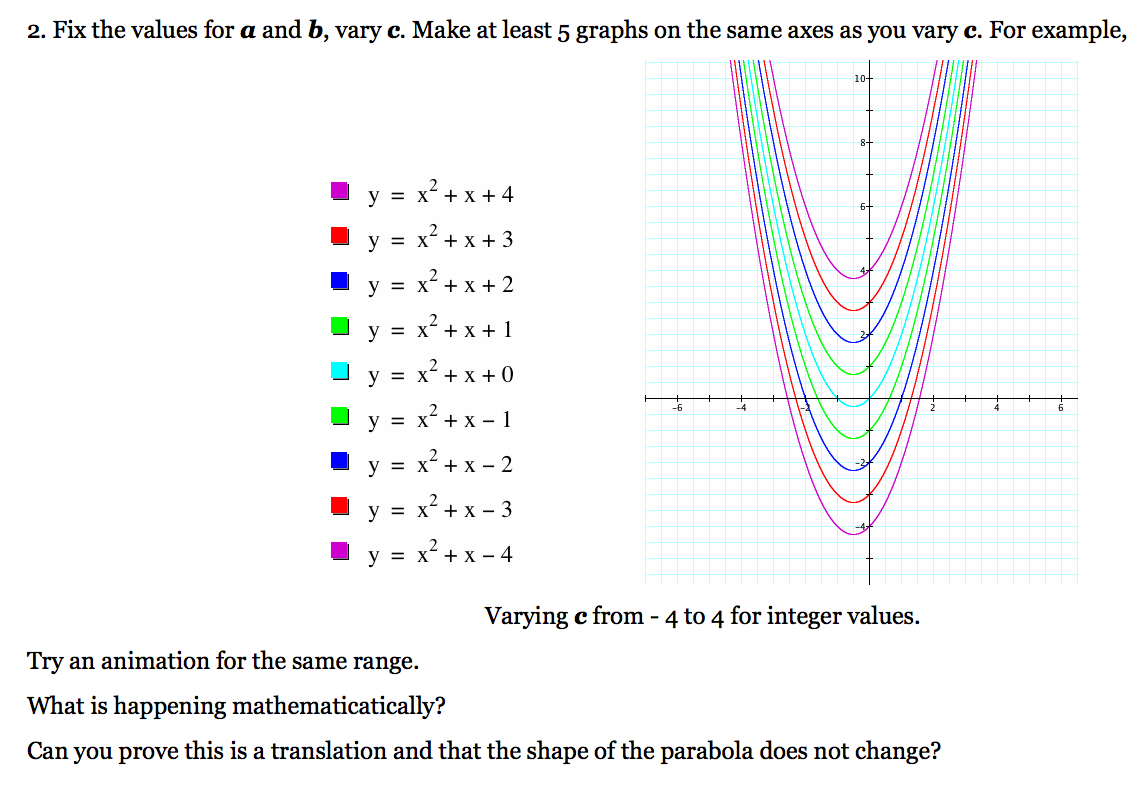
As you can see in the animation, there are three different graphs. The purple graph is the graph of our original equation as the value of c varies from -4 to 4. The red equation is x=
and the blue equation is y=c-(
). Based on these graphs it seems that as the value of c only changes the location of the vertex. The vertex seems to move up and down a vertical line at x=
. The point of intersection of the blue equation and the red equation is the location of the vertex of our function. We can see that the vertical line never moves horizontally, so the vertex of the funciton must shift up and down as the values of c changes. The horizontal, blue, line moves up and down as the function moves up and down, which is another indicator that the vertex of the function is shifting up and down the red line.
Mathematically we can see why this happens by taking the derivative of our funciton. The derivative of the funciton is (dy/dx)=2x+1, now we can set the derivative equal to zero and solve for x. This will give us the x-value at which our function has a horizontal tangent line which also gives us the x-value at which the vertex of our equation lies on. When you set the derivative equal to zero and solve you get x=
which corresponds to the graph of our red line in the animation. This tells us that the vertex moves along the line x=
because when x=
there is a horizontal tangent line, so our vertex must have an x-value of 
. We know the value of c does not have an effect on the x-value of the vertex because the derivative of a constant is zero, thus the value of c does not affect the derivative of our function because c is a constant. Now, we need to find the y-value of our vertex as the value of c changes. Since, we know the vertex will always have an x-value of 
, we can use this information to find the y-value of our vertex as c changes. If we substitute 
into our function for x, then we will find that y=c-(
), which is the path of the y-value of the vertex as c changes. This change in the y-value of the vertex is expressed by the blue graph in our animation. We can also see that the only change in our vertex is the y-value, so the y-value of our vertex is dependent upon the value of c. If c=(
), then the vertex of our function would lie on the x-axis because the y-value of the vertex would be zero. If c>(
), then the vertex of the function would lie on the line x=
and the y-value would be greater than zero, so the vertex would be above the x-axis. If c<(
), then our vertex would be below the x-axis on the line x=
. From our equation y=c-(
), we can see that as the value of c increases, the y-value will increase as well, thus shifting the graph up. As the value of c decreases, then the y-value will decrease, thus shifting the graph down. Therefore, the value of c shifts the graph up and down.
To prove this is a translation we can use our knowledge of derivatives to show the function never changes shape. As we know the output of the derivative is the slope of the tangent line at any value of x. As we mentioned earlier, the derivative of the function is (dy/dx)=2x+1. You can see that the derivative isn't dependent upon the value of c, this is because the derivative of a constant, c, is zero. Therefore, the value of c doesn't effect the slope of arbitrary x values. Therefore, we could substitute any value in for x and the value of the derivative, or the slope of the tangent line at the particular x-value, would remain constant for every value of c because the value of c doesn't affect the derivative. Now we can use this information to think about the shape of our funciton as the value of c changes. If the slope of every x-value in our function remains constant for every value of c, then the shape of our graph must be the same for every value of c. If the slope for an arbitrary x-value, say d, changed based on the value of c, then the shape would change, but since the slope remains the same, then the shape remains the same.