Assignment 4
Explorations of the Centroid
Drew Wilson
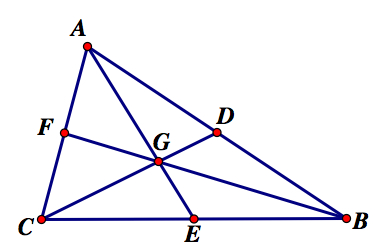The medians used to construct the centroid divide the triangle into six smaller triangles. Show that the area for each of these triangles are the same. Below is a figure that expresses the triangle ABC and the six smaller triangles formed by the construction of the centroid, G, of triangle ABC.
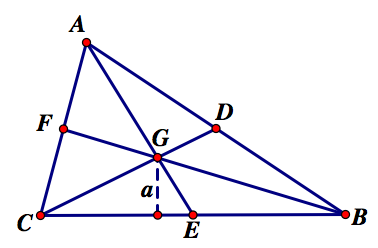
First, we know the formula for area of a triangle is one half of the base multiplied by the height, or altitude, of the triangle. We also know that points D, E, and F are the midpoints of their respective side. Therefore, we know segment AD=DB, CE=EB, AF=FC.
Say we let the base of each triangle be the side of the triangle that is shared with one of the sides of the original triangle. For example, the base for triangles CGE and EGB will be segments CE and EB which we know are the same. Now if we consider the formula for the area of a triangle we can see that the area of triangle CGE=the area of triangle CGB because they have the same base and the same height as shown to the right. Line segment, a, represents the altitude for both triangles CGE and EGB because the altitude is created by a line segment perpendicular to the base of the triangle through the vertex opposite the base of the triangle. As we can see from the figure, we know the altitude will be the same for both triangles because the vertex opposite the side of the base for both triangles is the point G, and segment, a, is perpendicular to CE and EB. Therefore, since the altitude and the base are the same for each triangle, the area of both triangles are the same.
Similarly if we consider triangles AGF and FGC, we would let segments AF and FC be the base for each triangle and point G would be the vertex opposite the base that would be used to create the altitude for each triangle. Once again, since each triangle have the same base and altitude the area for each triangle will be the same. The same occurs for triangles ADG and DGB if we let segments AD and DB be the base and G be the vertex opposite the base that is used to create the altitude for each triangle.
Now we have three pairs of triangles that share the same area. We need to show that two different pair of triangles have the same area in order to show that all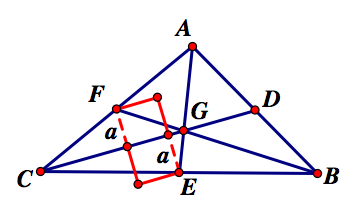 
six triangles have the same area. For example, we need to show that triangles CGB and CGF have the same area and triangles AGF and AGD have the same area, and from this we can conclude that all six triangles have the same area.
Let's consider triangles CGE and CGF and compare the area for each of these triangles. Let's define the base for each triangle as the line segment CG. Since each triangle shares this side, we know the base for each triangle is the same. Now, we need to consider the altitude for each triangle and determine if the altitude for each triangle is the same. We know that the altitude for each triangle will be perpendicular to the base, CG, so the altitude for each triangle will be parallel to each other. If we were to construct segments through each vertex of each triangle, F and E, perpendicular to the altitude, then we would have two line segments of equal length. Now, if we were to extend each altitude to the newly constructed segments, then we would have constructed a rectangle. We know this is a rectangle because each side is parallel to the opposite side and perpendicular to the adjacent side. We also know that each angle is 90 degrees because opposite sides are parallel. We also know, based on our construction, that the line segment CG intersects this rectangle in such a way that the rectangle is divided into two equal parts because CG is the base of each triangle and is the basis for the construction of each altitude. Since line segment CG divides the rectangle into two equal parts, we know that the altitudes for each triangle are equivalent. If the altitude for triangle CGE were shorter than the altitude of triangle CGF, then we would have constructed a quadrilateral that is not a rectangle because adjacent sides would not be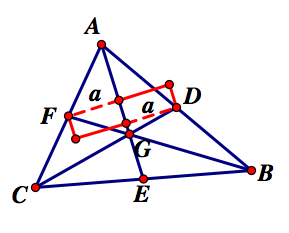
perpendicular. An example of the rectangle formed by the two altitudes is show at the right. As you can see the altitude for each triangle is given by segment a and the base CG divides the rectangle into two equal parts.
Similarly, if we consider triangles AGF and AGD, and we set segment AG as the base for each triangle, then the altitude for each triangle will be the same as well. We could also construct rectangles from the two altitudes as we did before and show that segment AG divides the rectangle into two equal parts which provides the result that the two altitudes are equivalent. An example is given to the right. Now that we have shown that triangle CGE has the same area as triangle CGF, then we can conclude that triangles EGB=CGE=CFG=FAG all have equal area. Since the area triangle FAG=the area of triangle AGD, we can conclude that triangles FAG=AGD=GDB and since the previous conclusion we know that triangles EGB=CGE=CFG=FAG=AGD=GDB all have the same area. Therefore, each of the six smaller triangles formed by the construction of a centroid have the same area.