Assignment 7

Tangent Circles

Drew Wilson

In this write-up we will explore and investigate properties of tangent circles. There are three main cases we have to consider when trying to construct a circle tangent to two given circles. If we are given two different cirlces and a point on one of the cirlces can we construct a circle tangent to the two circles? As a matter of fact, we can construct two circles that will be tangent to the two given circles, but first we need to discuss the different possibilities of the two given circles.

I.) One of the given circles could lie inside of the other given circle

II.) The two given circles could be overlapping

III.) The two circles could be disjoint

We will notice in our explorations that there will be two tangent circles to the given circles. One circle will be internally tangent and the other tangent circle will be externally tangent, they will be specified in the write-up.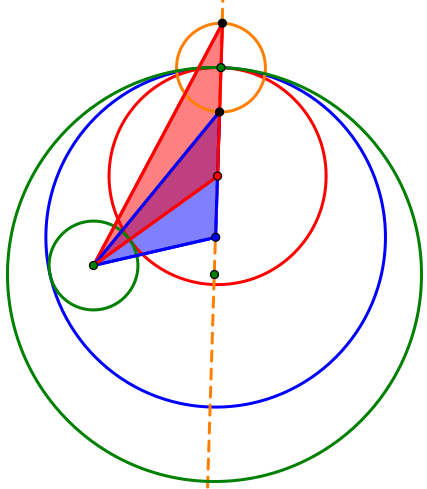 

Before we begin to explore the different types of tangent circles, let's explore the construction of the internal and external tangent circles. The construction for the internal and external tangent circles is the same for all three cases above. We are given two different circles and a point on one of the circles and we want to construct two circles that are tangent to the two given circles.  First we will construct a line through the center of the circle and the point on the circle. Now we can use this line to determine where the centers of the two tangent circles will lie, the centers of the two tangent circles lie on this line. We can use an isoceles triangle to help us find where the center should be because we want to find a point on this line equidistant from the point on the circle to a point on the other circle. If we construct a circle with the center as the given point on the circle and a radius equal to the radius of the circle without a point, then we can canstruct our isoceles triangle.  Construct points where our newly constructed circle (orange) and the constructed line (orange) cross. If we construct line segments between the intersection of the orange cirlce and the orange line then construct perpendicular bisectors to these two segments. The centers of the two circles will be the intersection of the perpendicular bisectors and the orange line. The figure to the right shows the construction. The two isoceles triangles that are formed are shaded in the color of the tangent cirlce they belong to. The red circle is internally tangent, and the red isoceles triangle corresponds with this circle. The blue circle is externally tangent and corresponds with the blue isoceles triangle. The orange cirlce and line are also showed and the green point is the point on the circle that is given.

Case I.)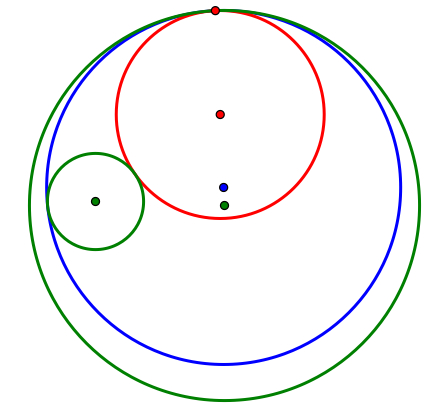

To the right is a picture where the two given circles are shown in green, with their centers shown in green as well, and the two tangent circles are red and blue with their centers corresponding in the same color. As you can see the red circle is internally tangent because it lies inside both green circles. The blue circle is externally tangent because one of the green circles lies inside of the blue circle. In this case both tangent cirlces lie inside of the larger given circle, but this doesn't always happen as we will see later in this write-up. Here is a link you can use to explore my findings on GSP. If you select the centers of the two given circles, marked by the color green, then you can change the size of the circles and also show the other two cases as well. If you would like to explore more about tangent circles click here.

Case II.)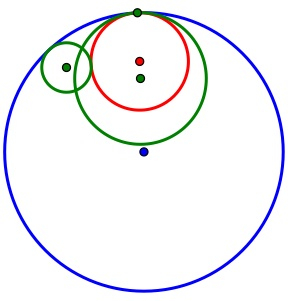

To the left is a picture where the colors are represented the same as in case one. The two circles in this case are overlapping as you can see, but there are still two different tangent circles. The red circle is internally tangent and the blue circle is externally tangent. In this case you can see that the two given circles are inside of the externally tangent circle, and the internally tangent circle remains enclosed by one circle. If you would like to explore more click on the link in case one and change the two green circles in such a way that they are overlapping, then you can explore with different size circles.

Case III.)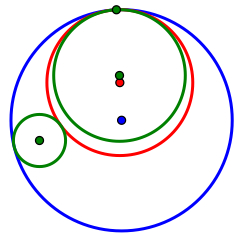

To the right is a picture of the third case, which is when the two given circles are disjoint. The colors still correspond the same way they did in case one and case two. The red circle is still internally tangent and the blue circle is externally tangent. This case is similar to case two because the blue circle is still outside of the two green circles, but the red cirlce is no longer enclosed by one of the green circles. Here we can see that the internally tangent circle encloses one of the green circles which is usually what the externally tangent circle does, but since the externally tangent circle encloses both circles, the internally tangent circle can't be considered externally tangent.

Let's consider the loci of the centers of the two tangent circles.

If we use GSP to trace the centers of the two tangent circles and animate the given point, then we will see that the loci for the two tangent circles are ellipses. For case II, the locus of the internally tangent circle is an ellipse and the locus of the externally tangent circle is a hyperbola. For case III, the loci of the two tangent circles are hyperbolas. From this we can make a generalization that if the tangent circle lies within one of the given circles, the locus will be an ellipse and if the tangent circle lies outside of one of the circles, then the locus will be a hyperbola. In this write-up we will only focus on case I.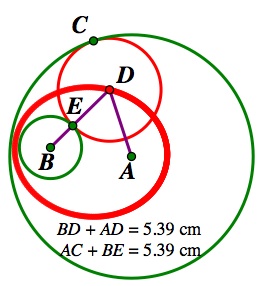

To the right is a picture that shows the locus of the internally tangent circle. The foci of the ellipse are the centers of the two given circles. We know this is an ellipse because if we take a point on the ellipse and we add the distance from the point to both foci we will get a fixed value. The fixed value is equal to the sum of each radius of the two given circles. As you can see in the picture to the right, the distance betwee the foci and a point on the ellipse is equal to the sum of the radii of each of the given circles.

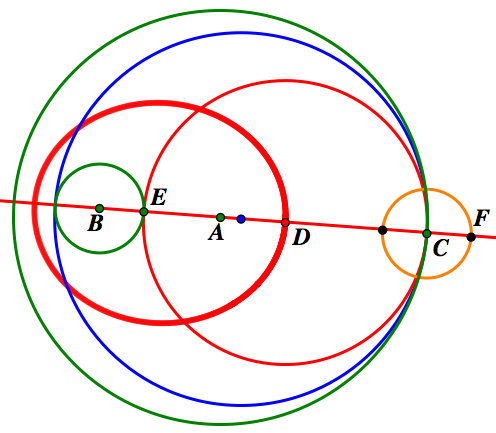
We can see this by looking at a special case when the center of the tangent circle lies on the line that the two foci lie on. This will enable us to see that the locus is an ellipse. The figure below is a picture of the special case. As you can see there are points A, B, C, D, E, and F in the figure where points A and B are the centers of the two given circles as well as the foci of the ellipse. Point C is the point on the circle given at the beginning of the problem, and point D is the center of the internally tangent circle which is located on the ellipse. Point E is a point on the circle with center B and point F is a point on the circle with center C. In this case, if we consider the length from each foci to point D, we will find that the length remains fixed as the sum of the radii of the two given circles (green circles). As you can see in the figure below, through this special case we can show the distance from the foci to point D is equal to the sum of the radii of the two green circles. We know that length BD=FD and we know that length AD is fixed. Now if we calculate the distance from the foci to point D the same way we did above, then we will have length BD+AD, which is equal to length AF. We know that AF is the sum of the radii of the two circles because in our construction we constructed the circle with center C to have the same radius as the given circle with center B. Therefore, we know AF consists of radius AC and radius BE=CF, thus the length AF is equal to the sum of the length of the two radii of the given circles. Therefore, we know the locus of the internally tangent circle is an ellipse. A similar argument follows for the externally tangent circle.

Return