Assignment 8

Ratios of the Altitudes of an Acute Triangle

Drew Wilson

Above is the task we will work with in this write-up.

Let's prove the first part of the task:

Proof:

Let X be the area of triangle ABC

Then:                                           

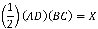
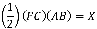
We know that X can also be calculated by adding the areas of triangles BHC, AHB, and AHC because these three triangles make up triangle ABC.

Now we have:                   

If we divide by X, we get:   

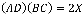
We know that                and         by manipulating our area of triangle ABC for each formula.

Now if we substitute (AD)(BC) for 2X in the first part of our previous equation, (FC)(AB) for 2X in the second part of the equation, and (BE)(AC) for 2X in the third part of our equation, we get:

Now we know that BC divides to be one in the first part, AB divides to be one in the second part, and AC divides to be one in the third part leaving us with:

Thus, our claim has been proved.

Let's prove the second part of the task:

Proof:

We know that HD = AD - AH, HE = BE - BH, and HF = CF - CH.

Now if we substitute these values into the equation from part one, we get:

Now if we separate each fraction we get:

Since AD divides to one, BE divides to one, and CF divides to one, we are left with:

Now, if we manipulate our equation, we arrive at:

Thus, our claim has been proved.

 

What if triangle ABC is obtuse?

If triangle ABC is obtuse, then we know the orthocenter will lie outside of the triangle. If the orthocenter is outside of the triangle, then the argument fails and can't be proved. This argument only holds for acute triangles because the orthocenter lies inside of the triangle if and only if the triangle is acute. If the triangle is a right triangle, the orthocenter will lie on one of the vertices, and the argument will not hold for this case as well.

Return