

Assignment 9
Pedal Triangles
Drew Wilson
If we construct triangle ABC, and we construct the pedal triangle with the pedal point on one of the sides of triangle ABC, what will we observe? What if the pedal point is on one of the vertices of triangle ABC, what will we observe?
What if the pedal point is on one of the sides of triangle ABC?
We know that in order to construct the pedal triangle you extend each side of triangle ABC so that each side is a line. Then you construct a point, called the pedal point. You construct lines through the pedal point and perpendicular to each side of triangle ABC, and where the perpendicular lines intersect the extended side of triangle ABC will be the vertices of the pedal triangle.
Let's consider acute triangles.
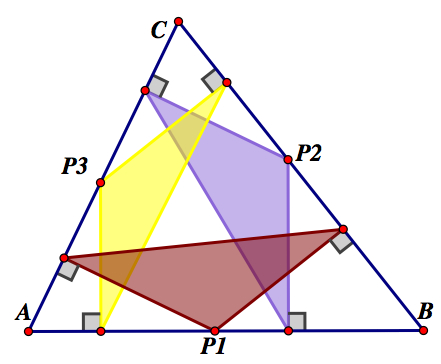
Now, if we locate the pedal point on one of the sides of triangle ABC, then we know that the pedal triangle will be formed by the intersection of perpendicular lines through the pedal point and perpendicular to each side of the triangle. We can make the assumption that since each side of the pedal triangle is formed by these perpendicular lines, the two vertices of the pedal triangle, not the pedal point, will form right angles with the corresponding side of triangle ABC. We know that the pedal point is one of the vertices of the pedal triangle because the pedal point is on one of the sides of triangle ABC, thus the pedal point will be the point of intersection of the line through the pedal point and perpendicular to the side of the triangle the pedal point lies on. The right angle will not be part of the pedal triangle because the pedal triangle will be acute since triangle ABC is acute, so the right angle will be the exterior angle of the two vertices, not the pedal point. The picture below shows where the right angles are located and where the pedal points are located. The pedal points are P1, P2, and P3. If you would like to explore more with this construction click here. You can click and drag the three pedal points and notice the shapes of the pedal triangles and also notice that the right angles never change. You can also change the size of the triangle by selection one of the vertices, A, B, or C, and moving the vertices. Notice what happens when the triangle becomes obtuse.
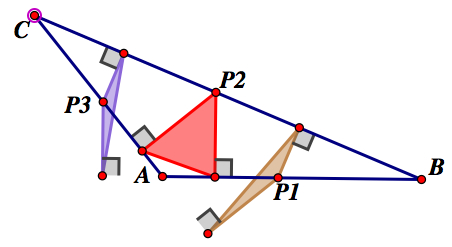
If we consider obtuse triangles, we will observe something quite different. If triangle ABC is obtuse and the pedal point is along one of the sides, then only one pedal triangle remains inside of triangle ABC. The pedal triangle with pedal point opposite the obtuse angle remains inside of the obtuse triangle. The other two pedal triangles are partially inside of triangle ABC, but each triangle has a vertex outside of triangle ABC. Similar to the acute case, the pedal triangles form two right external angles. The pedal triangle that lies inside of triangle ABC, has the two external right angles on the sides of the other two vertices. The other two pedal triangles only have one external right angle along one of the sides of triangle ABC with the other external right angle lying on the extended sides of triangle ABC. You can click on the link in the acute triangle exploration and change the size of the triangle to form an obtuse triangle to explore more about the pedal triangle formed when the pedal point is along one of the sides of triangle ABC. The picture below is an example of the pedal triangles formed when the pedal point is along the sides of an obtuse triangle.
What if the pedal point is on one of the vertices of triangle ABC?
Let's consdier acute triangles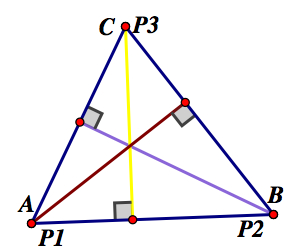
We can use what we know about the construction of pedal triangles to make inferences about what may happen when the pedal point lies on one of the vertices of triangle ABC. Since the pedal triangle is formed by the lines through the pedal point and perpendicular to each side, and since the pedal point is on one of the vertices, the pedal triangle will be a line. We know the pedal triangle will be a line because the pedal point shares a point with two of the sides of triangle ABC, therefore, the lines through the pedal point and perpendicular to these two sides will give the same point which is the pedal point. The other point is given by the intersection of the line through the pedal point and perpendicular to the opposite side of the pedal point. Since the triangle is acute, each of the three lines formed will lie inside of the triangles and each line will form a right angle with the side opposite the pedal point. We can generalize this phenomena by saying that when the pedal point lies on one of the vertices of a triangle, the pedal triangle will be the altitude of the triangle through that vertex. The picture to the right shows that the pedal triangles formed when the pedal point lies on the vertices of the triangle are the altitudes of the triangle through the corresponding vertex. The triangle is labeled the same as before with the pedal points as P1, P2, and P3.
If we consider obtuse triangles and the pedal point lies on the vertices of the triangle, then the pedal point located on the vertex of the obtuse angle will construct the altitude inside of the triangle. If the pedal point lies on one of the other two vertices, then the altitudes will lie outside of the triangle. If the triangle is a right triangle and the pedal points lie on the vertices of the right triangle, then there will only be one altitude inside of the triangle with the pedal point located on the vertex of the right angle. If the pedal points lie on the other two vertices, then the altitude is given by the side lengt from the vertex, or pedal point, to the vertex of the right angle. You can explore this by clicking on the link provided in the first paragraph of this write up.