Assignment 12
Fibonnaci Sequence
Drew Wilson
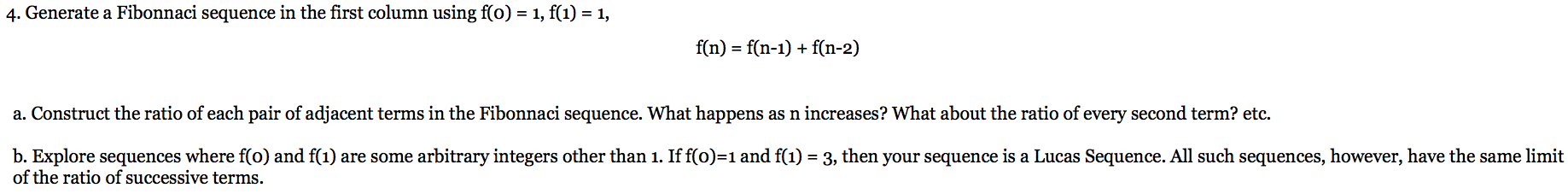
In this write up we will explore ratios of the Fibonnaci sequence.
Here is a look at the Fibonnaci sequence for the first 35 values of x and the corresponding y value associated with the equation.
Now we will look at the ratio of the adjacent terms of the Fibonnaci sequence. The ratio will be provided in the third column of the picture below.
Notice that as the value of x gets larger, then our ratio tends to a certain value 1.61803399 which is approximately the value of the golden ratio provided by the following calculation:
.
Now let's look at the ratio of every second term in the Fibonacci sequence.
Here we can see again that the ratio is approaching one value which is 2.61803399. How is this value associated with the previous ratio? It looks like we could just add a value of 1 to the golden ratio to arrive at our conclusion, but it goes a little deeper than that. We can see the relationship with this number and the golden ratio by looking at the value of this calculation :
which is approximately the value that the ratio of every second term approaches.
Now if we look at every third term we will see that the value that the ratio approaches follows the pattern. The ratio of every third term approaches the value of the following calculation :
.
Based on what we have observed with these examples we can make the conclusion that as we take the ratio of every nth term of the Fibonacci sequence we will notice that the ratio of every nth term approaches the value calculated by the follwoing :
.
What if we started our sequence with different values for f(0) and f(1)? What do you think will happen with our ratio? I think that as long as we are using the same formula as the Fibonnaci sequence we will contine to get the same results. Thus the ratio of every nth term will be represented by the following equation :
As you can see the ratios stayed the same even though our value for f(0) and f(1) changed. This makes sense because we are using the same formula, but different values, so we should arrive at the same result.
Even if we let f(0) be greater than f(1) we will see that the ratios still approach the same values. Below is an example when f(0)=3 and f(2)=2. I was interested to see if the ratio would change if we made the initial term greater than the first term, but the ratios stayed the same as you can see below.
