Equations of Parabolas

Colleen Foy

The two standard forms of a parabola are:

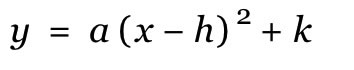
Let's explore the first form first: . Graphing this in Graphing Calculator we obtain the following graph:

The graph above shows the parabolas when b = 1, c = 1, and when a = -3, -2, -1, 1, 2, and 3. The parameter a plays the following role in the standard form of a parabola:

              If a > 0, the parabola opens up

              If a < 0, the parabola opens down

              If  | a | > 1, the parabola widens (compresses)

              If  | a | > 1, the parabola narrows (stretches).

Next, we can explore what happens when we leave a = 1 and c = 1 and change the b parameter:

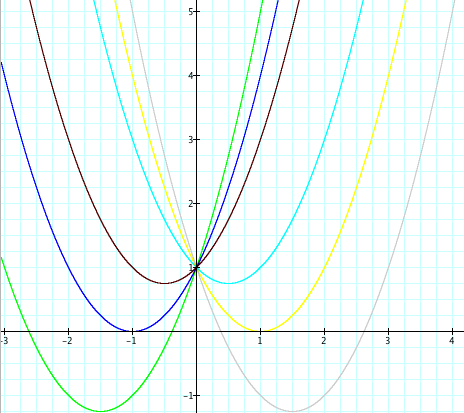
Changing b changes the axis of symmetry of our parabola. The axis of symmetry is defined by the line: . So, the orientation of the parabola changes as b changes. Next we can explore how c affects the parabola.

Changing c shifts the parabola up and down. Note that in the graphs above, a = 1 and b = 1.

Here is a movie demonstrating what happens to a parabola as a changes from -10 to 10 (b=1 , c=1):

Here is a movie demonstrating what happens to a parabola as b changes from -10 to 10 (a=1 , c=1):

Here is a movie demonstrating what happens to a parabola as c changes from -10 to 10 (a=1 , b=1):

 

The second form for the equation of a parabola is vertex form. Vertex form is as follows:

In vertex form, the coordinate ( h , k ) is the vertex. As in the other form:

If a > 0, the parabola opens up

              If a < 0, the parabola opens down

              If  | a | > 1, the parabola widens (compresses)

              If  | a | > 1, the parabola narrows (stretches).

Let's explore what happens when we change a, k, and h.

Here is a movie showing the change in a while h=1 and k=1:

Here is a movie showing the change in h while a=1 and k=1:

Here is a movie showing the change in k while a=1 and h=1:

 

Now we will explore how to derive one formula from the other. Starting with the standard form of a parabola, we can complete the square to obtain the vertex form.

Note that in the second and last lines, we renamed to be h (which is the x-coordinate of the vertex) and to be k (which is the y-coordinate of the vertex). Thus we derived the vertex form from the standard form.  

 

return