

Tangent Circles
Colleen Foy
For this problem we are given two circles and a point on one of the circles. We are to construct a circle tangent to both of the given circles with one point of tangency being the designated point. First we start with the given:
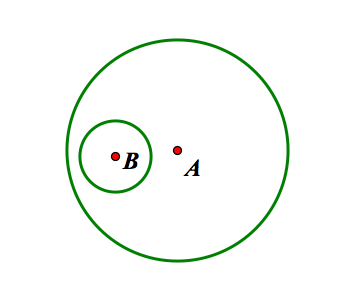
Our goal is to construct a circle tangent to both of these circles. Let C be the desired point of tangency. Now construct a line through A and C, and a line segment for the radius of the circle with center B.
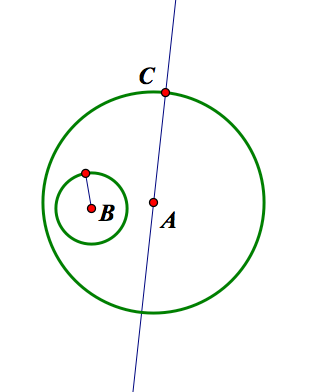
Now construct the circle with center C and radius EB. Then construct the line segment BD. Construct the perpendicular bisector of BD. The point G will be the center of the circle tangent to the original two circles.
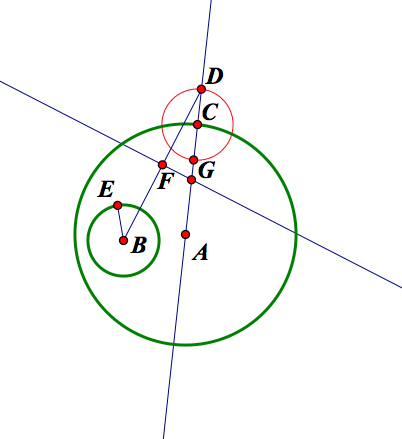
Construct the circle with center G and radius GC.
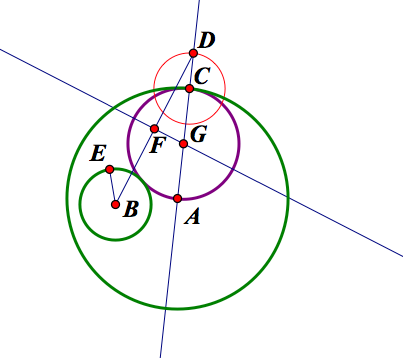
Here is a look at the final product.
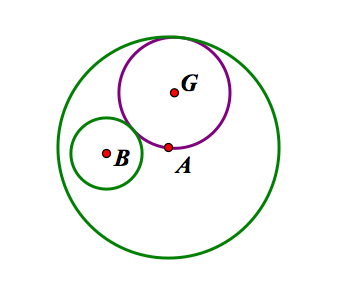
Now, watch what happens when we trace G and animate the point C.
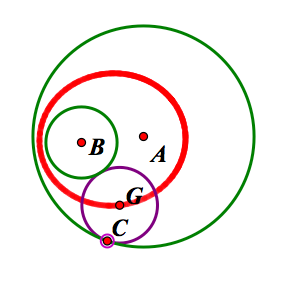
It appears that G forms an ellipse when C is animated around the circle. Let's prove that. Let T be the point of tangency with the inside circle. Construct the segment GB and CA.
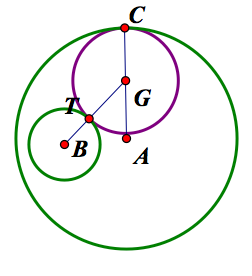
In order for the path of G to be an ellipse, we must prove that the sum of the distance from G to two fixed points is constant. We know that B and A are both fixed points because they are the centers of the two circles that were given to us. Note that AC is the radius of the larger circle, and BT is the radius of the smaller circle. GT and GC are both radii of the tangent circle. Thus, GC = GT. Since AC = AG + GC, by segment addition, we know that AC = AG + GT by substitution. We also know that GB = BT + GT by segment addition. Thus we deduce that AG + BG = AC - GT + BT + GT = AC + BT. Since we have shown that AG + BG = AC + BT, we have shown that the sum of the distance from the center of the big circle to the center of the tangent circle and the distance of the center of the tangent circle to the center of the small circle is equal to the sum of the radii AC and BT which remain fixed. Hence, the path of G forms an ellipse.
Let's explore what happens when the second circle lies outside of the big circle. Using the same method as we did before, we obtain the following (the red circle is the tangent circle).
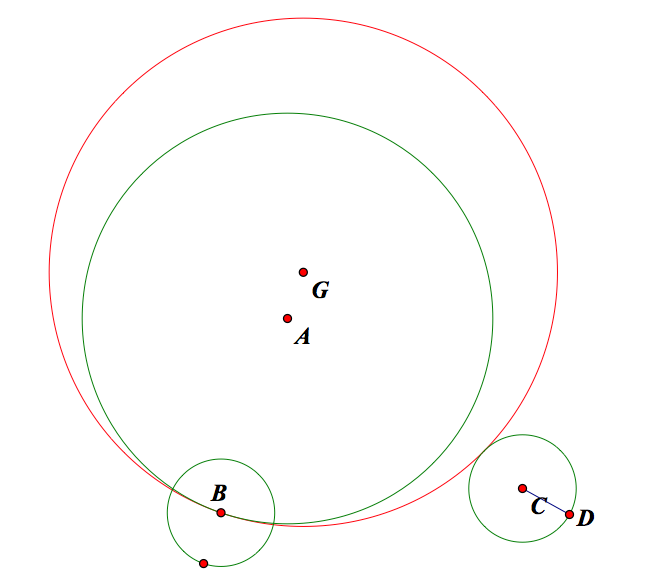
Again, if we were to animate point B, what would the path of G look like? Click here for the animation GSP file.
Note that the path of G in this scenario appears to be a hyperbola rather than an ellipse. Can we prove this?
To show that the path of G (the center of the tangent circle) is a hyperbola, we need to show that the difference from G to two fixed points in constant. Refer to the following picture:
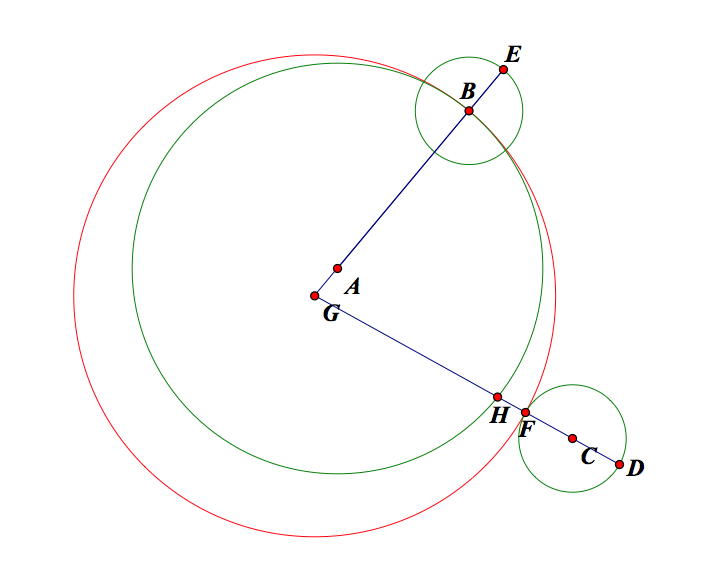

In other words, we want to show that GC - GA is equal to a constant. We know that A and C are fixed because they are the centers of the original circles. Also, observe that AB is the radius of the big (given) circle, and CD is the radius of the small circle. Note that GB = GF because they are both radii of the same circle. By segment addition we know that GB = GA + AB and GF = GH + HF. We also know that GC - FC = GB. Thus by substitution, we know that GC - FC = GA + AB. After some algebra we obtain GC - GA = AB + FC. Since AB and CD are radii, their sum is also constant. Hence we have shown that the difference of distance from the center of the tangent circle G to the center of the small circle C is equal to a constant. In conclusion we have shown that the path of the center of the tangent is a hyperbola when the small circle is outside the larger circle.