Altitudes and Orthocenters

Colleen Foy 

Given an acute triangle ABC. Construct the Orthocenter O. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully.

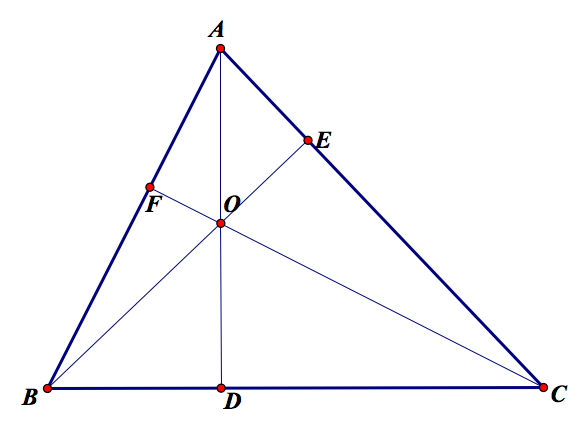
Prove:

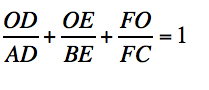
Note that: .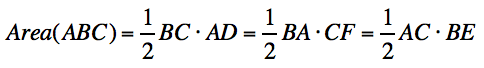

The area of the triangle ABC is equal to the sum of the areas of the triangles inside:

Dividing both sides of the equation we obtain:

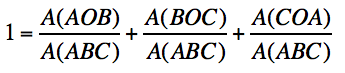
By substitution we obtain: .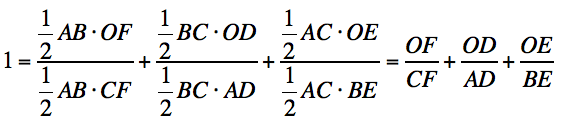

Prove: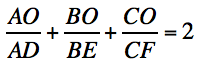

Note that: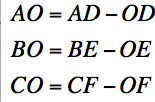

Thus by substitution and algebra we obtain:

(From the previous proof)

What happens when triangle ABC is obtuse?

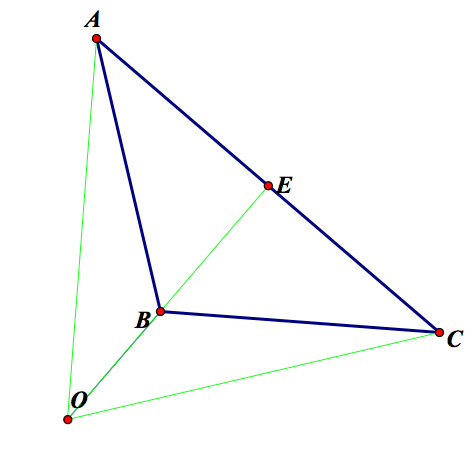
When triangle ABC is obtuse, The orthocenter O lies outside of the triangle. In this case, the points D and F are not visible. This is due to the fact that they lie on the lines AB and BC, but not on the segments. Thus. the two proofs do not hold for an obtuse triangle.