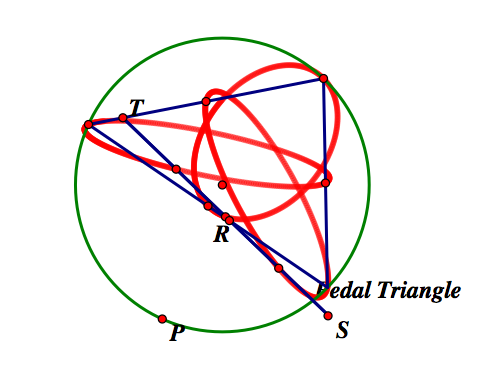
Pedal Triangles
Colleen Foy
Suppose we are given a triangle ABC and a point P anywhere in the plane. Construct the perpendicular lines from P to the sides of ABC. Label the intersections R, S, and T. Triangle RST is called the Pedal Triangle of point P. Click here for a script tool of the Pedal Triangle give points A,B,C, and P.
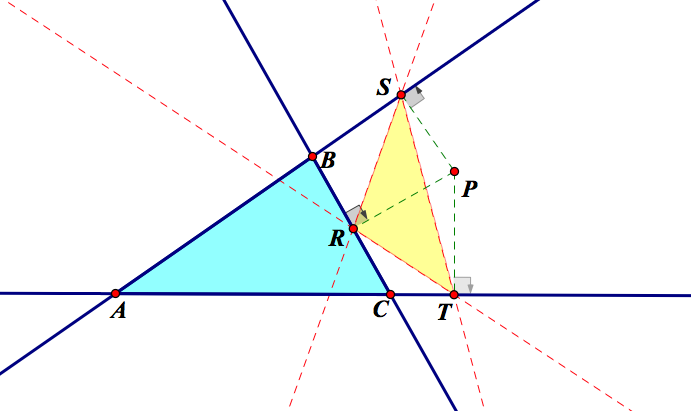
Observe what happens when the Pedal Triangle is inside triangle ABC.
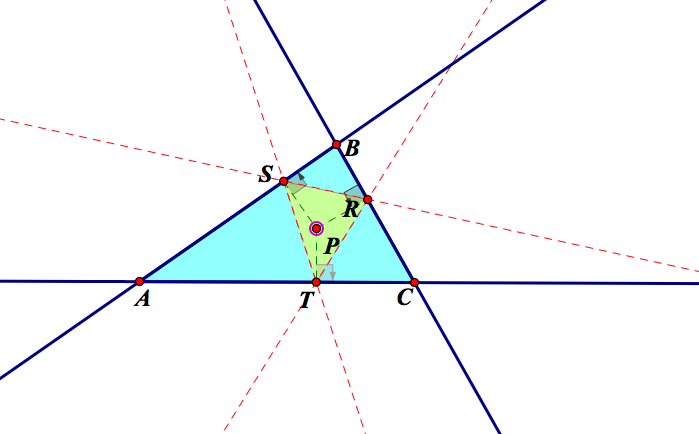
Now, construct the midpoints of the Pedal Triangle and construct the circumcenter K of triangle ABC. Trace the midpoints of the pedal triangle as P is animated around a circle with a radius larger than the circumcircle of triangle ABC. Click here for the GSP file of this animation.
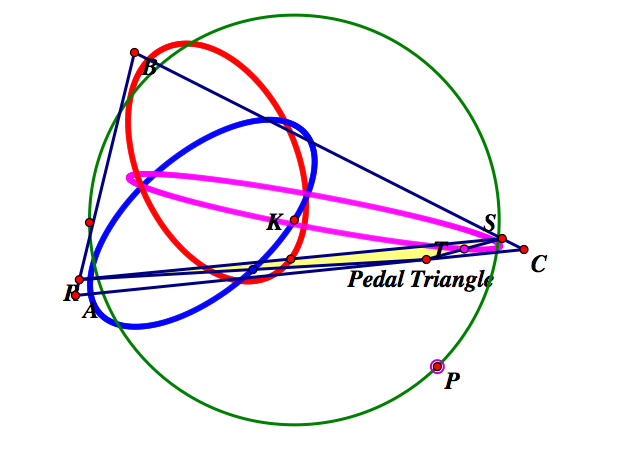
As seen above, the paths of the midpoints of the pedal triangle are all ellipses. What would happen if the circle we traced P around was smaller than the circumcircle of triangle ABC?
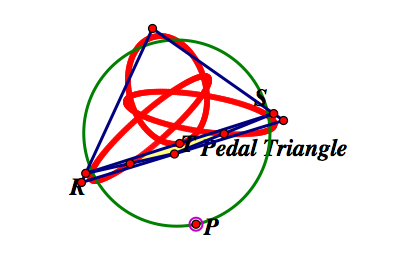
What if P is traced around the circumcircle of triangle ABC? Click here for an animation.