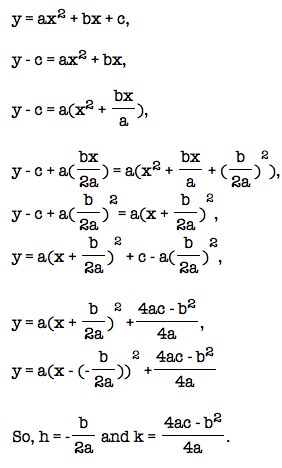Standard Forms of Parabolas
By: Lacy Gainey
Geometric Definition of a Parabola: A parabola is a set of points in the plane equal distance from a point and a line.
This point is called the Focus and the line is called the Directrix.
Observe the GSP construction. Drag point (x, k-p) and observe what happens.
Notice, that no matter where we drag point (x, k-p), the distances between the Focus and point (x, y) and the Directrix and point (x, y) are equal.
Now, lets set these distances equal to each other and see what we find.
Using the distance formula, 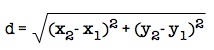 , we will set these distances equal to each other.
, we will set these distances equal to each other.
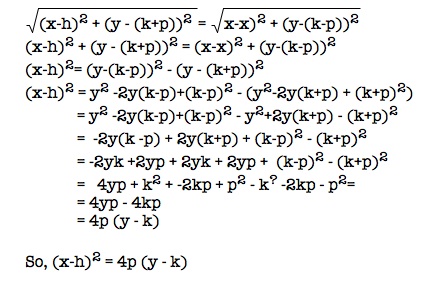
-
This equation,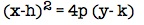 ,is in Standard Form and is called the vertex form of the parabola.
,is in Standard Form and is called the vertex form of the parabola.
Looking at the GSP construction and the vertex form of the parabola, we can use the GSP construction and the vertex form of the parabola to find the vertex, focus, and directrix, in addition to the roles of parameters, h, k, and p.
Vertex: (h, k)
Focus: (h, k + p)
Directrix: y = k – p
-
Example: Identify the vertex, focus, and directrix of 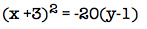 .
.
4p = -20, p = -5
Vertex: (-3, 1)
Focus: (-3, -4)
Directrix: y = 6
-
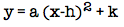 is also a standard form of the graph of a parabola. This equation in vertex form as well.
is also a standard form of the graph of a parabola. This equation in vertex form as well.
Notice that h represents a horizontal translation of the parabola and k represents a vertical translation of the parabola.
What does a represent? Compare the graphs of the functions 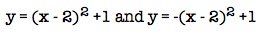 .
.
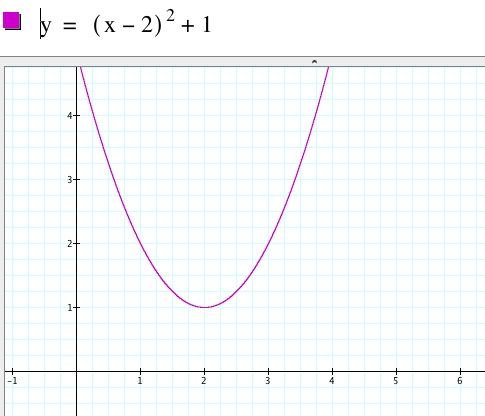
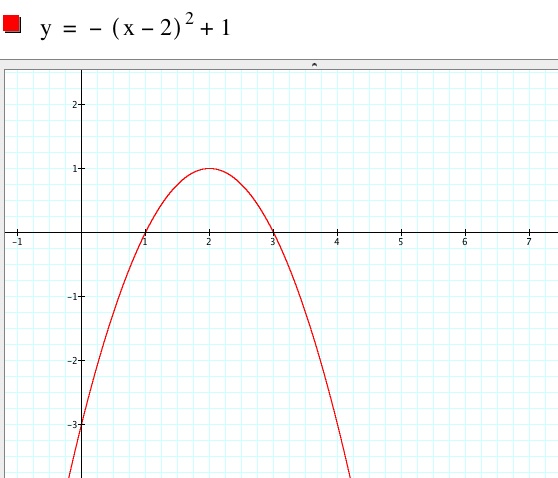
From the graphs, we can see that a affects the openness of the parabola. Additionally, if a is positive the parabola is pointed up and if a is negative the parabola is pointed down.
We can use this standard form, 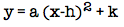 , to find the vertex, line of symmetry, and maximum/minimum value of the parabola.
, to find the vertex, line of symmetry, and maximum/minimum value of the parabola.
Vertex: (h, k)
Line of Symmetry: The line of symmetry is located at the vertex. Since we are dealing with parabolas that are pointed up and down, the vertex is located at x = h.
Maximum/Minimum: The maximum or minimum is located at the vertex of the parabola. So the maximum or minimum will be k. This point will be a maximum if the parabola is facing downwards and a minimum if the parabola is facing upwards.
-
Example: Identify the vertex, line of symmetry, and maximum/minimum value of y = 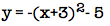 .
.
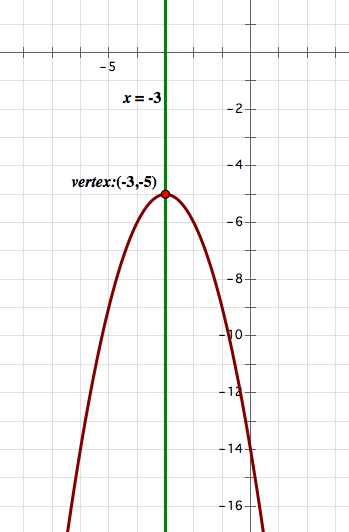
Vertex: (-3, -5)
Line of Symmetry: x = -3
Maximum/Minimum Value: Maximum value (because a is negative and the parabola is facing downwards) at y = -5.
-
Could we use this standard form, 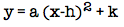 , to find the focus and directrix of the parabola as well?
, to find the focus and directrix of the parabola as well?
-
What is the relationship between a in 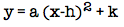 and 4p in
and 4p in 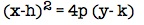 ?
?
-
Manipulating the formula, 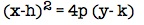 ,
,
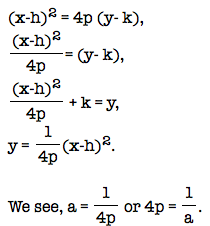
Using this relation, we could determine p. We would then be able to determine the focus and directrix of the parabola.
We have determined that we can use the standard forms, 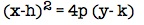 and
and 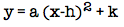 , to identify the vertex, line of symmetry, maximum/minimum, focus, and directrix of a parabola.
, to identify the vertex, line of symmetry, maximum/minimum, focus, and directrix of a parabola.
We should now determine how we arrived at the equation in the form 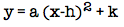 .
.
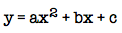 in addition to
in addition to 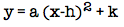 represent parabolas. Since both of these equations represent parabolas, we should be able to derive one from the other.
represent parabolas. Since both of these equations represent parabolas, we should be able to derive one from the other.
-
Lets derive 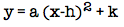 from
from 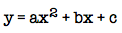 by completing the square.
by completing the square.
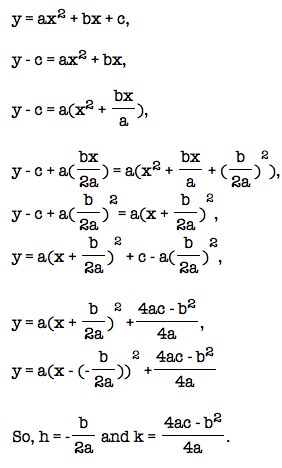
We have discussed the roles of a, h, k, & p. Above, we discovered the roles b and c played in the determination of h and k.
Lets explore b and c further:
-
Hold a and c constant at a = 1 and c = 0 and observe the affect of b.
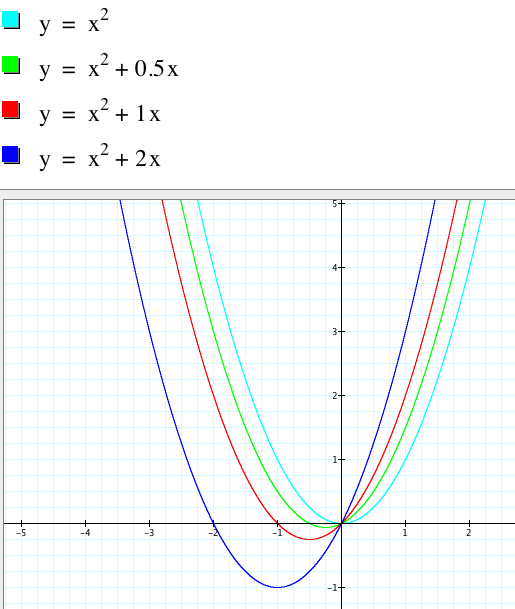
Looking at the graphs above, b seems to affect the placement of our vertex.
-
Hold a and b constant at a = 1 and b = 0 and observe the affect of c.
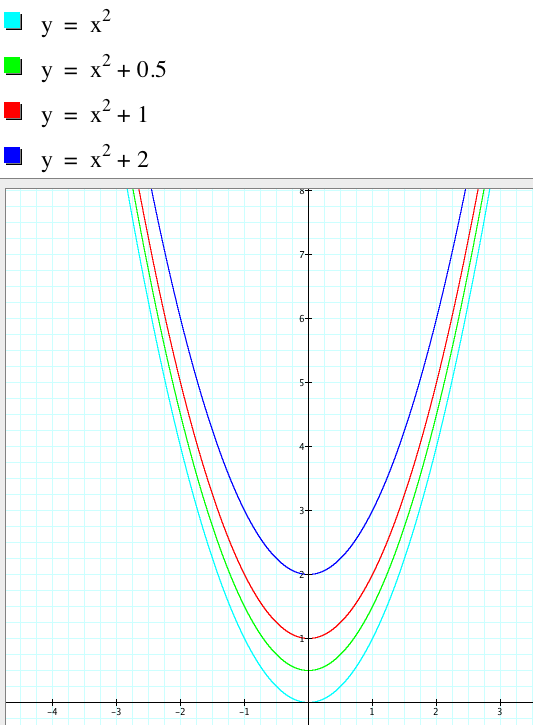
Looking at the graphs above, we can see that c affects the placement of our vertex as well. Additionally, c also seems to represent a vertical translation.


, we will set these distances equal to each other.
.
.
, to find the vertex, line of symmetry, and maximum/minimum value of the parabola.
.
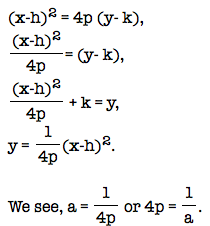
and
, to identify the vertex, line of symmetry, maximum/minimum, focus, and directrix of a parabola.
.
in addition to
represent parabolas. Since both of these equations represent parabolas, we should be able to derive one from the other.