Finding the Sum of Consecutive Natural Numbers

by: Maggie Hendricks

A very common and popular problem in secondary mathematics is that of finding the sum of the first n natural numbers. The problem is rich in the mathematics it can involve and produce, and it is for this reason that it is something that requires further study. The closed form formula for determining the desired sum is a commonly known one (n(n+1)/2), but what is interesting is the many different ways that we can derive that formula. In this essay, we will take a look at five such ways of deriving this formula.

First let’s look at writing out the sum of the first n natural numbers twice, once as [1+2+3+…+(n-2)+(n-1)+n] and once in “reverse” [n+(n-1)+(n-2)+…+3+2+1]. If we imagine stacking these two representations on top of each other and adding up the corresponding columns, the result will be as seen below:

  1+2+3+…+(n-2)+(n-1)+n

+n+(n-1)+(n-2)+…+3+2+1

(n+1)+(n+1)+…+(n+1)+(n+1)

Each of the columns creates a sum of (n+1), and it can be fairly easily seen that there are n such terms that have been developed. This would mean the total result would be n(n+1). However, we should remember that this was found from taking the sum of the first n natural numbers TWICE, and we should divide the previous total in half to gain our desired result.

Thus, we see that 1+2+3+…+(n-2)+(n-1)+n = n(n+1)/2

For our second look at deriving this formula, we will take a geometric approach. It should also be noted that we will make use of notation associated with the triangular numbers. The triangular numbers are a set of numbers that result from adding the first n consecutive natural numbers. We represent the nth triangular number with the notation T(n), and we know that T(n) is equal to T(n-1)+n. To begin, we will look at the first few triangular numbers represented by the dot diagrams as shown below:

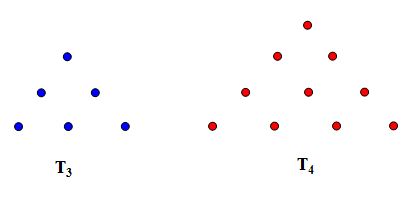
If we were to combine these two diagrams together, they would form a square, as shown below.

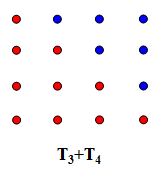
We can see that the dimensions of the above square are 4 by 4. Thus, we can say that T(3)+T(4)=42. We could generalize this to become T(n-1)+T(n)=n2. Recursively, we also know that T(n)=T(n-1)+n. Manipulating this formula a bit, we can see that T(n-1)=T(n)-n. We can then substitute this value into our first equation to see that T(n)-n+T(n)=n2. Combining some like terms, we see that 2T(n)-n=n2. Again, using some algebraic manipulation, we could arrive at T(n)=n(n+1)/2, where T(n) is equal to the sum of the first n natural numbers.

Our third approach to deriving the closed formula is similar to the second, but instead of looking at combining two consecutive terms, we will look at taking two of the same term. Consider the dot diagram below representing the sum of the first 4 triangular numbers.

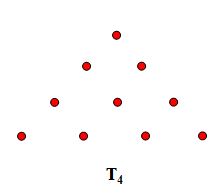
We then want to consider what would happen if we took two of this diagram and put them together forming a square. The result can be seen below (note that the different coloring is used simply to identify the first diagram from the second).

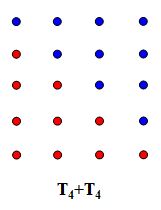
We can see that the dimensions of the square that is formed when taking twice T(4) is 4 by 5. In other words, 2T(4)=4(4+1). We could generalize this to say that 2T(n)=n(n+1). It is easy to see from here that T(n)=n(n+1)/2, where T(n) represents the sum of the first n natural numbers.

Our fourth look takes an algebraic approach to deriving the formula. Take the expression 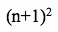. By expanding this expression, we arrive at the result shown below:

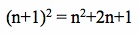
This can be algebraically manipulated to say that

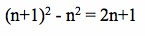
Since the above equation is true for n, it should also be true when we replace n with n-1, n-2, n-3, …, 2, 1. See the resulting equations from these replacements below:

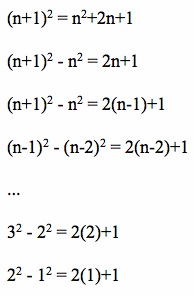
If we add each of these equations together, we will see that on the left side of the equation all the terms cancel with one another except for the first, 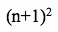, and the last, .

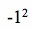On the right side of the equation, we see the sum of the first n natural numbers multiplied by a factor of 2, and a term of 1 repeated n times. Putting it all together gets us the result below:

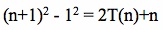
Expanding and combining like terms leads us to the result below:

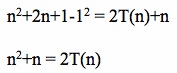
T(n) = n(n+1)/2, where T(n) represents the sum of the first n natural numbers.

For our fifth and final look at deriving the closed form formula for the sum of the first n natural numbers, we will start by taking a look at the sum of the first n integers squared (from 0 to n) as well as the first n integers squared (from 0 to n+1). Note that the first sum is equal to the second sum minus the term 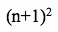. We can represent this algebraically as seen below.

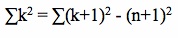
If we expand the term 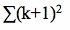, the result is the following:

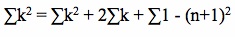
Combining some like terms and moving some things around gets us the following:

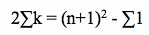
It can be noted at this point that taking the sum of 1 for the first n integers produces the result of n+1. Substituting this value into our equation above gives us:

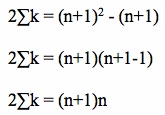
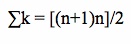, where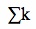is our desired sum of the first n natural numbers.

Although this essay in no way exhausts the potential ways to approach finding the sum of the first n natural numbers, it is a good start in showing the variety of ways that it can be shown and may also give some ideas for extension activities and related concepts associated with the problem.

Click here to return to Maggie's homepage.