Points on a Circle

by: Maggie Hendricks

This essay takes a look at several interesting concepts and problems that arise from looking at a circle with n points on its perimeter. There are several ideas to explore relating to this, but this essay specifically takes a look at three things:

1. Given a circle, what is the number of chords determined by n points on its perimeter?
Note here, that chord refers to the segment joining any two points together, as seen below.

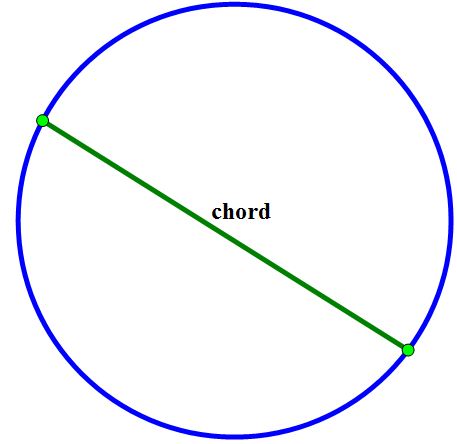
2. Given a circle, what is the number of diagonals determined by n points on its perimeter?
Note here, that diagonal refers to any chord that also serves as the diagonal of an inscribed polygon, as shown below.

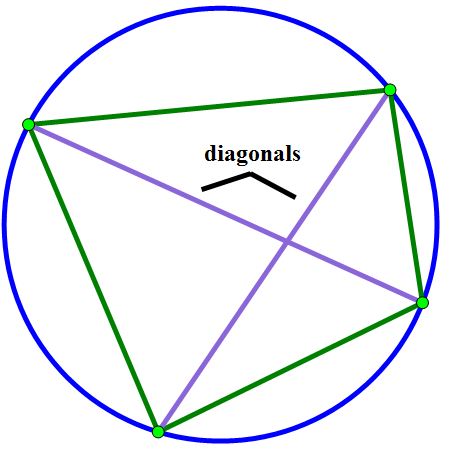
3. Given a circle with n points on its perimeter, what is the maximum number of regions determined by the chords and the circle rim?
See the figure below for a visual representation of what is meant by the term region used above.

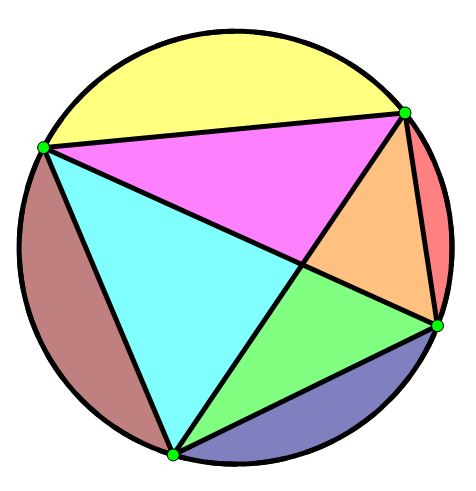
To begin, let’s take a look at answering the first question. Starting with the case when n is equal to zero and continuing through the case when n is equal to five, the diagrams shown below can get us started with exploring the number of chords.

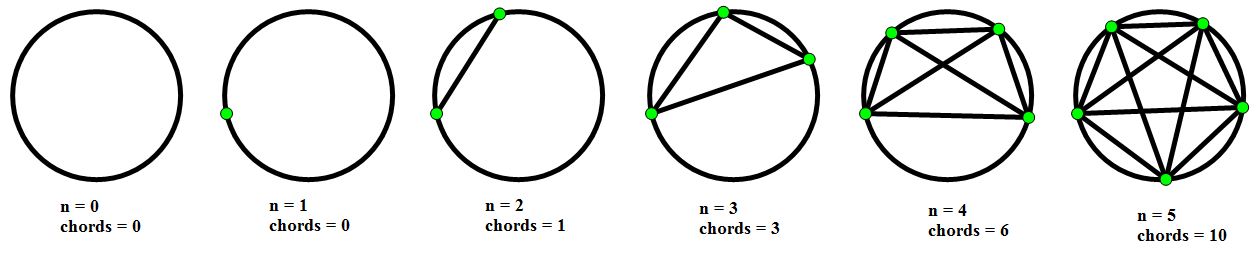
We might notice here that once the possibility for an initial chord is created (when n is equal to 2), the difference between the number of chords for the consecutive cases afterward increases by one each time. This would lead us to expect the number of chords determined by a circle with 6 points on it would be 10 + 5, or 15, and we would also then expect the number of chords determined by a circle with 7 points on it to be 15 + 6, or 21. A quick look at the diagram below will show us that we are correct in our assumption.

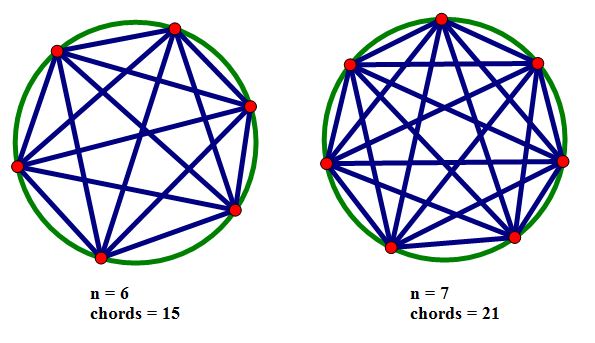
It would be fairly easy to reason through why the pattern seen above would continue for each increasing case for n. As stated earlier, the possibility of an initial chord is created when n is equal to 2. When we increase to 3 points on the circle, we still have the initial chord, but we must now also create new chords connecting the third point to each of the others (so n – 1 new chords are created); this gives us a total chord number of 3. Increasing the number of points to 4, we would still have all of three previous chords, and we would need to create new chords connecting the fourth point to the other three (so n – 1 new chords again). This pattern continues, because each time a new point is added, we can think of it as taking the previous number of chords and adding n – 1 to it in order to get the total number of chords determined by that number of points.

An interesting fact to take note of here that this pattern is not a random or unique pattern. The recursive set of integers created by adding n – 1 to the previous term is also known as the Triangular Numbers (also referred to as).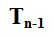

Now let’s take a look at the number of diagonals determined by n points on a circle. As noted earlier, a diagonal here is meant to describe a chord that also serves as the diagonal of an inscribed polygon. Since the first case that this would be possible for is the case when n is equal to 4, we can start there. Using logic (and a visual), we can see that the number of diagonals for any circle with n points (as long as n is greater than or equal to 4) is the number of chords minus the chords forming the outside of the polygon in consideration. The number of chords forming the outside of the polygon is the same as the number of points (since there would be one chord connecting each point to the next as we move around the perimeter of the circle). We could use this logic to write a formula for finding the number of diagonals determined by a circle with n points; this formula would be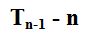. For the cases when n is equal to 0, 1, 2, or 3 the number of diagonals can be said to be equal to zero; these are also the values when our formula would give us a negative (and therefore unrealistic) value. To check a few cases that will help us be sure our formula works, see the figures below.

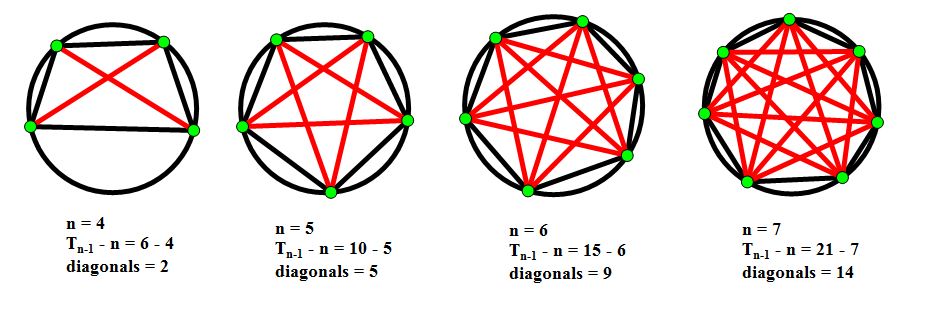
The third problem to be looked at in this essay is one where a simple explanation or formula will not capture the pattern seen. However, let’s take a look at what can be said about the maximum number of regions determined by the chords and circle rim of a circle with n points on it.

Obviously, the initial case when n is equal to zero results in one region (the interior of the circle). When n is equal to one the number of regions remains zero, since no chords can be created to split the interior of the circle. When n is two the number of regions becomes two; when n is three the number of regions becomes four; when n is four the number of regions becomes eight; when n is five the number of regions is sixteen. It might be tempting at this point to say that the maximum number of regions is equal to two raised to the power of n – 1 (as long as n is greater than or equal to one). See the figure below for a visual to go along with our ideas so far.

It should be noted that the use of color above is simply to help the reader notice the different regions being counted; regions of the same color do not indicate that they are the same region, or that they are even regions of equivalent area.

If we go along with our idea mentioned above, we would expect the maximum number of regions for a circle with six points on it to be 32, but refer to the figure below to see that it is not so.

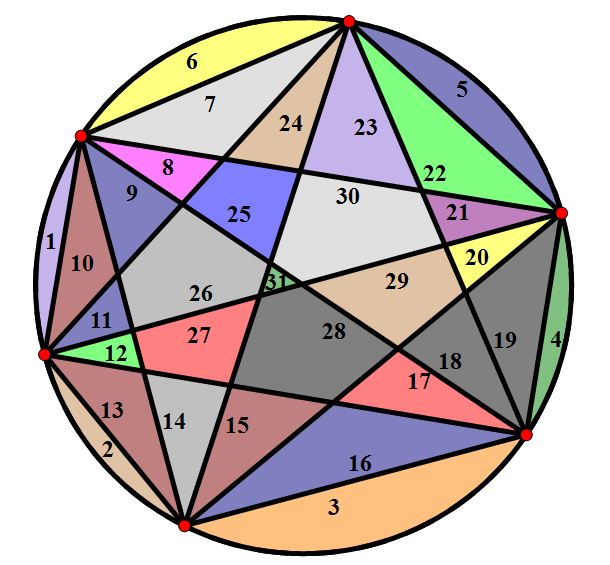
So our first idea might be shot now, but that does not mean that there is not some pattern to it. If we were to draw out the example for the case when n is equal to seven, we would be able to count and find that the maximum number of regions is 57. Similarly, if we were to draw out the example for the case when n is equal to eight, we could see that the maximum number of regions is 99. While this may not immediately give us any new ideas about what the pattern might be, a further look will reveal the following trend using a portion of Pascal’s Triangle. See the diagram below for an explanation.

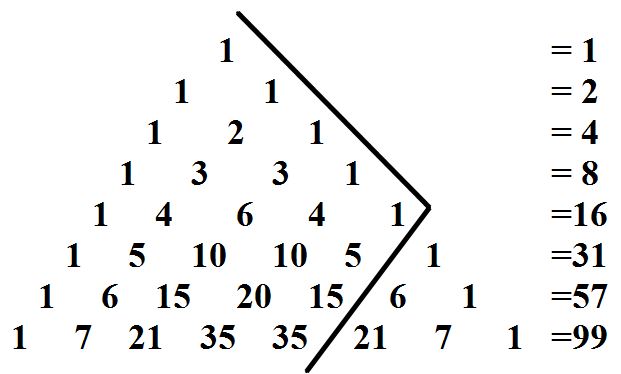
If Pascal’s Triangle is split as shown above, and then only the numbers to the left of the division are added in rows, the result will give us the pattern we have so far seen for the first seven cases of n and the maximum number of regions determined. Whether or not this pattern can be said to be a rule (that is, whether it continues for the following consecutive cases for n) is up to the reader to determine. Is there an explanation behind this strange pattern?

There are many interesting and puzzling ideas and concepts that can be unearthed when looking at a circle with an increasing number of points placed around its perimeter. While this essay makes an introduction to three such ideas, it is up to the reader to continue on and find other such interesting discoveries.

To return to Maggie's homepage, click here.