Fibonacci Sequence and Ratios

by: Maggie Hendricks

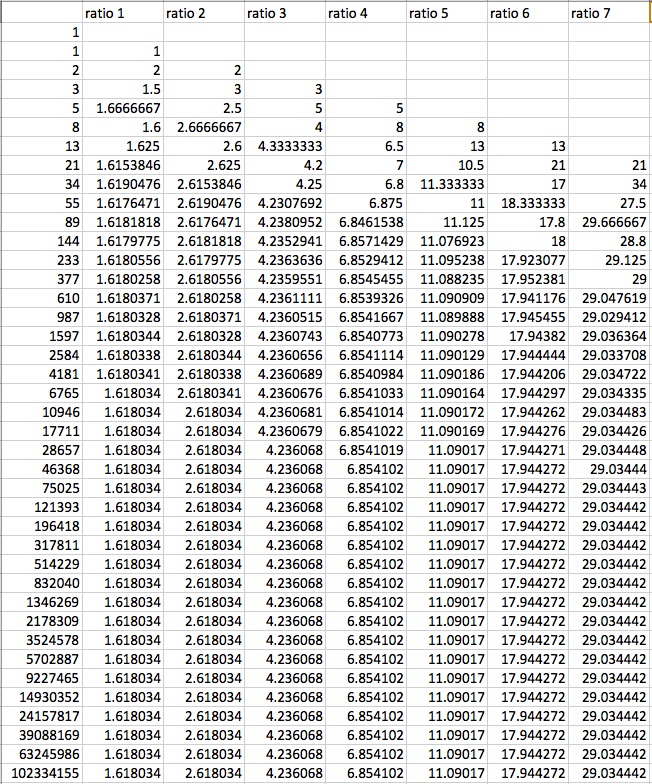
Using Excel, we can generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1, and f(n) = f(n-1) + f(n-2). In the second column we can construct the ratio of each pair of adjacent terms in the first column. We see that as n increases in this column, the ratio appears to be approaching the Golden Ratio (otherwise known as phi). In the third column we can construct the ratio of every second term; we see here that as n increases, the ratio appears to be approaching the square of the Golden Ratio (phi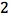). We can continue this pattern by taking the ratio of every third term in the fourth column, the ratio of every fourth term in the fifth column, through the ratio of every k 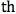term in the k+1 column. In each of these columns, we see the limit as n approaches infinity appears to be the Golden Ratio taken to the power of k (phi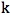). See the snapshot of an Excel spreadsheet below to see the values and trends discussed above.

What happens if we let f(0) and/or f(1) be something other than 1? We can repeat the same process as with the Fibonacci Sequence, and see that the limit of the ratio of successive terms is still equal to the integer powers of the Golden Ratio. See the snapshot of two Excel spreadsheets below for examples when f(0) and f(1) are not equal to 1.

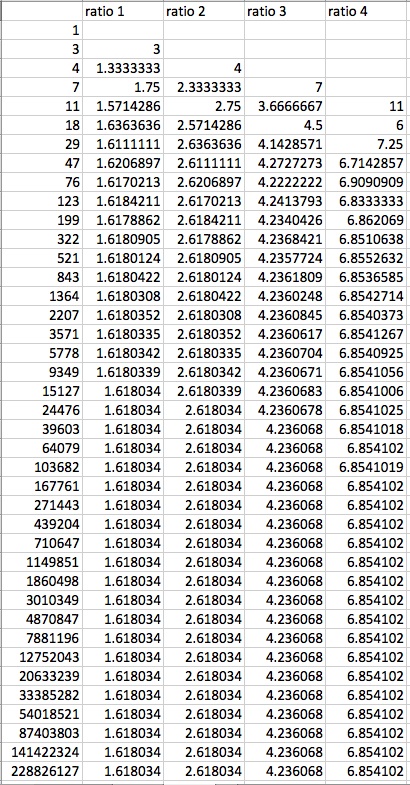
f(0) = 1 and f(1) = 3

(known as the Lucas Sequence)

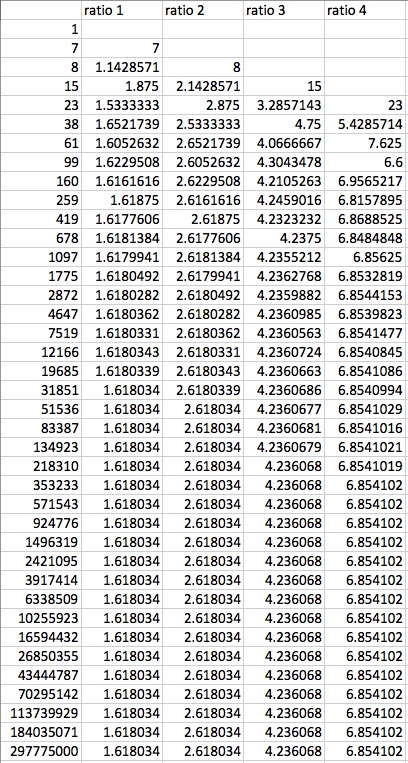
f(0) = 1 and f(1) = 7

Click here to return to Maggie's homepage.