Roots of Quadratic Functions in the x-b Plane
by: Maggie Hendricks
The general form of a quadratic function is typically given by the equation =ax2+bx+c.JPG)
. A common exercise in secondary mathematics classes is to have students find the “roots” that occur when the equation is set equal to zero (that is, the x-value or values that correspond to a y value of zero). To explore when and where these occur, let’s take a look at some patterns in graphs of this form in the x-b plane (that is, let the parameter b take on the role of dependent variable). To start, let’s look at the graph of 
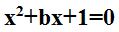(note that a = c = 1 here).
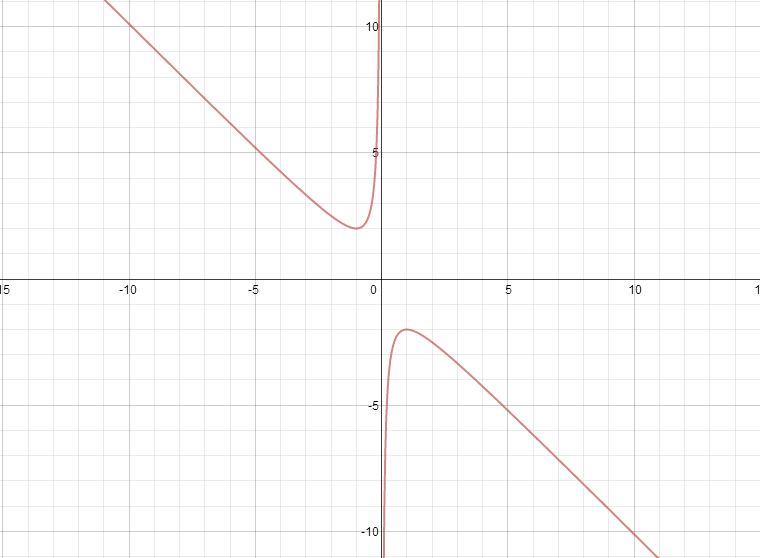
We see that the graph is a hyperbola with two asymptotes. We can fairly easily recognize that one of these asymptotes is the line x = 0. The other appears to be linear as well, but to determine what the linear function it, we can add the graph of our function when c is equal to zero (that is, the function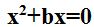 
).
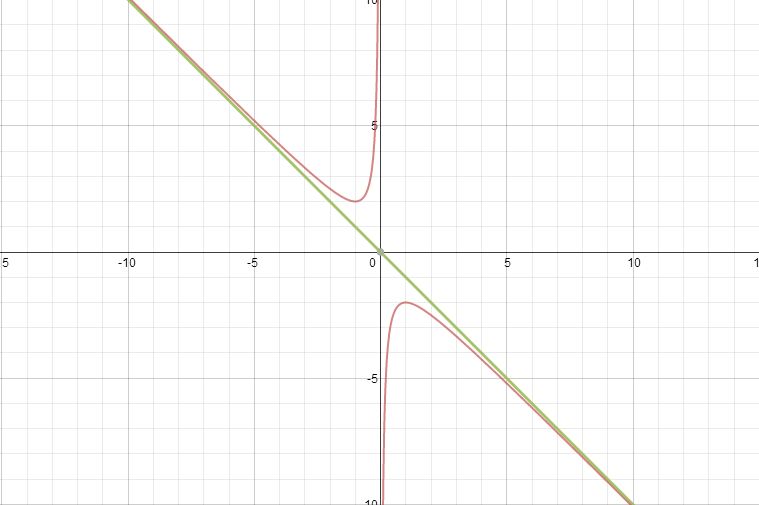
From this graph we can see fairly easily that our second asymptote is the line x = -b. Next, let’s graph some more functions for other values of c (say, c = 3, 5, and 7).
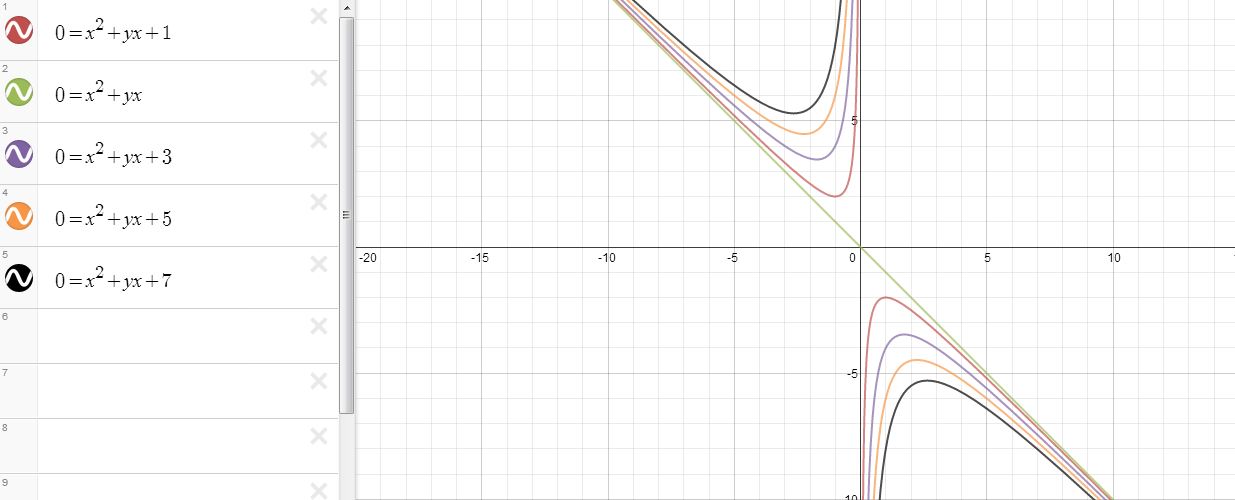
We see that these graphs are also hyperbolas, and we see that they also have two asymptotes (x = 0 and x = -b). Now where do the roots occur, and what generalizations can we make about them? Let’s take our latest graph and look at specific values of b; that is, let’s add horizontal lines for b = 5, b = 2, and b = 1.
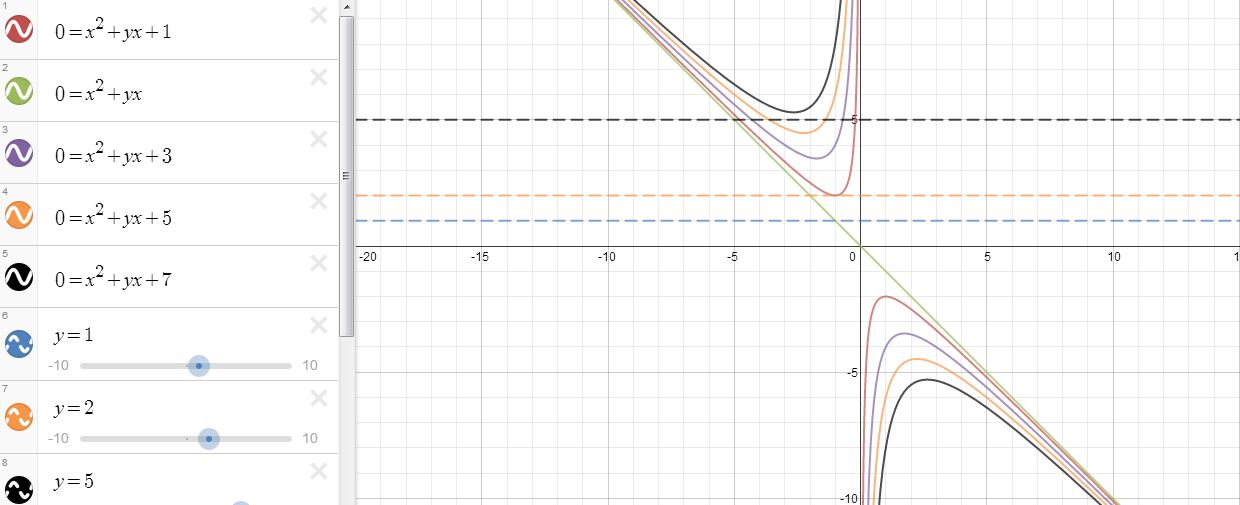
The points of intersection for these horizontal lines and any of our previous hyperbolas are the root or roots of that particular function for that particular b value. For example, the two points where the line b = 5 intersects the graph of 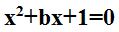are the roots for that function when b is equal to 5. We see that for each function, there are either two roots (two intersection points), one root (one intersection or point of tangency), or no roots (no intersection points).
When will there be no roots, one root, or two roots? If we look just at the original function 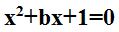we can see that there will be no real roots for any values of b between -2 and +2. When b is equal to -2 or to +2, we see that there will be exactly one real root. When b is either less than -2 or greater than +2, we see that there will be exactly two real roots.
What happens when c takes on a negative value instead of a positive value? Let’s look at some graphs for negative values of c (say, c = -1, -3, and -5).
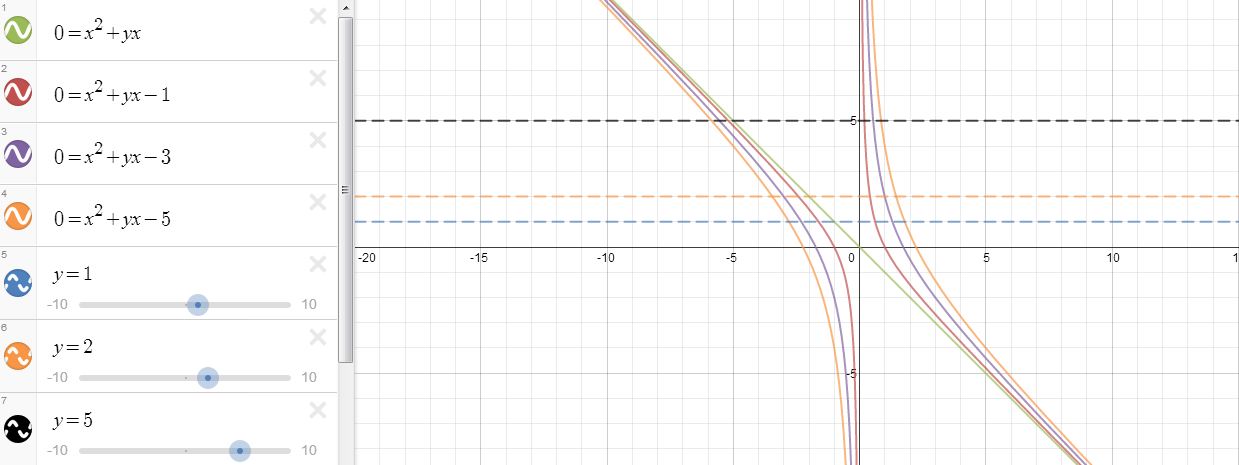
We see that the graphs are still hyperbolas, and we see that they still have asymptotes at the lines x = 0 and x = -b. Now, however, we see that for any values of b (our horizontal lines), these functions all have exactly two roots—that is, our horizontal lines intersect each of these hyperbolas at exactly two places. We can go a step further and generalize that for any value of b when c is negative there are exactly two real roots (one positive real root and one positive real root).
To summarize, when exploring the roots of a quadratic function in the x-b plane, we see that for any and all functions there will be either zero, one, or two real roots. For the function 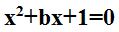there will be zero real roots for b values between -2 and +2, there will be exactly one real root when b is equal to -2 or +2, and there will be exactly two roots when b is either greater than +2 or less than -2. When the parameter c takes on a negative value, there will always be exactly two real roots for the functions.