
Relationships Created from the Altitudes of a Triangle
by: Maggie Hendricks
Given acute triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully.
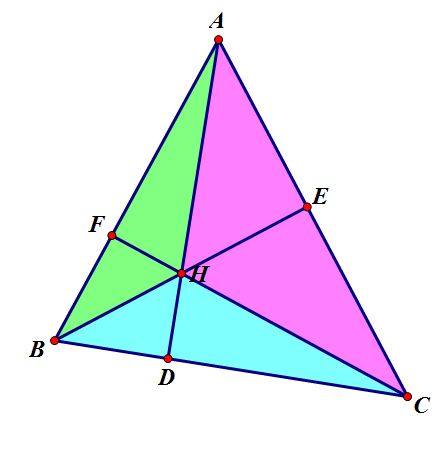
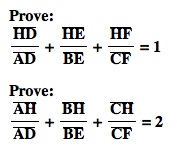
To begin the first proof, let’s look at some different ways we can represent the area of triangle ABC.
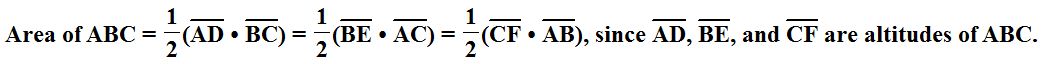
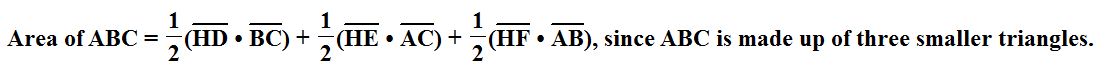
Since all parts of the first equation are equal, we can use them interchangeably as we manipulate the second equation. For example, we can take the second equation and divide through by the area of ABC (represented in different ways).
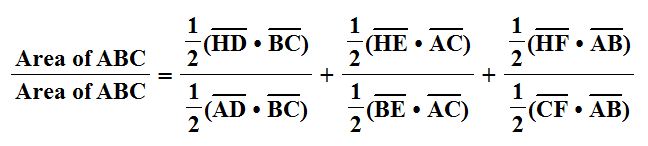
From here, we can simplify some to get the equation below, which is our desired result. Thus, we have proven the first equation is true.
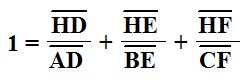
Now we can use this equation to start the second proof. Notice first the following relationships.
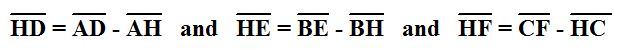
We can use these congruent representations as substitutions into our final equation from proof 1.
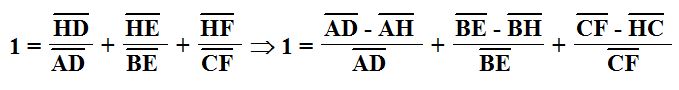
We can use these congruent representations as substitutions into our final equation from proof 1.
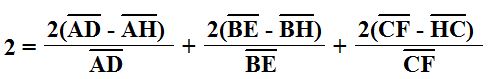
From here, we can separate some of the factors of our equation so as to allow us to manipulate it further.
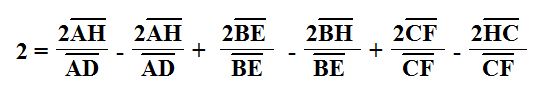
With some simplifying from here, we get the equation below.
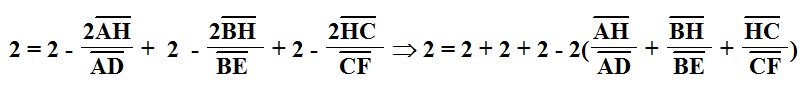
Now if we divide through our equation by a factor of 2, we get the equation below.
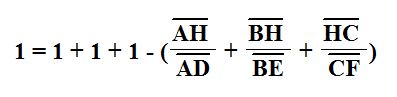
Now with the use of some inverse operations to combine like terms and eliminate any subtraction, we get the result below. This is our desired result; thus, we have proven that the second equation is true as well.
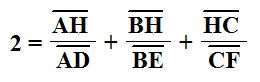
Now let’s consider what would happen if triangle ABC were obtuse. See the obtuse version of ABC below.
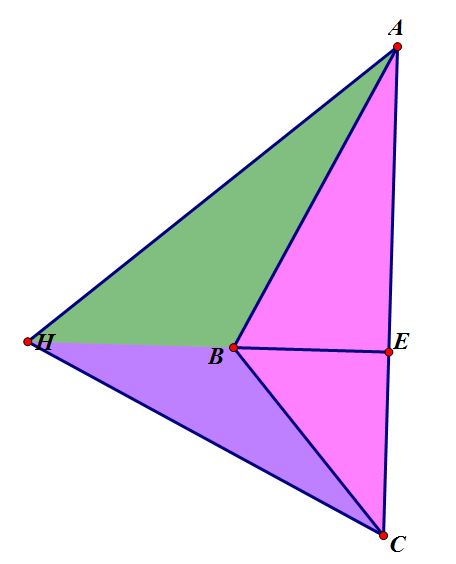
Notice that some of the segments used in both of our equations no longer exist. This is because the orthocenter (H) is now outside of the triangle, and the altitudes from points A and C no longer intersect a side of our triangle. It is because of this that our relationships no longer can hold true when triangle ABC is obtuse.

