In particular, given points A, B, & C such as those shown on the right (3 points and 2 segments that form an angle; in particular, such that AC is not vastly larger than BC, or vice versa), we seek to find points X and Y on segments AC and BC, respectively, such that AY =XY =XB. We here call segment XY an "equisegment." Such a segment is shown below:

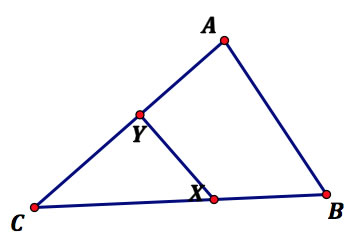X and Y were constructed using a method about to be shown.

They do indeed form an equisegment.

In order to construct the equisegment, I considered a few different methods. First, I looked at circles of various radii; would there be any way of systematically constructing the 2 points that lie on the intersection of two circles with the same radius but different centers? Given that we do not actually know the radius of the circles we desire nor wish our points X or Y to lie on the perpendicular bisector of segment AB, such a method proved futile.

Next, I considered whether or not segment XY was parallel to AB, and if this were true, wondered how this information might inform a construction. After both failing to make the construction and then seeing an example such as that given above (where segments XY and AB are quite clearly not parallel), I decided to go another route.

The key elements of this construction (or problem, if you will) that make it challenging are the fact that AC need not equal BC, and the fact that we cannot use trigonometry or any of the information about the angle ACB to inform a method - or at least not easily. It was then that it was suggested to me to make a guess for point X, construct the triangle for which it is an endpoint of the equisegment, and then use a dilation to project back to triangle ABC.

Before detailing this construction, let me first give a similar method that I tried with the assumption that segments XY and AB must be parallel, which I had still not let go of at the point of attempting the new "guess, correct, and dilate" method.

Consider the following. Suppose AC = BC. Then, given an equisegment XY, we have that AY = BX, and as a result,

CY = AC - AY = BC - AY = BC - BX = CX.

Hence, the equisegment XY would split the triangle ABC proportionally (the ratios of the side lengths would simplify to 1 = 1), and segments XY and AB would necessarily be parallel. Therefore, given A,B,C such that AC is parallel to BC, one can construct the first point, X, of the equisegment as follows:

1) Make a guess for Y and call it Y*. Select Y* such that AY* is greater than or equal to the distance from Y* to AB along a parallel line. In other words, select Y* such that the circle centered at Y* with radius AY* intersects side AB.

2) Construct the circle with center Y* and radius AY*.

3) Construct a line parallel to segment AB through Y*. Label the intersection of this line and the circle from the previous step X*.

4) Draw the line through A and X* until it intersects BC. Name this new point X.

Then X is one endpoint of the equisegment, and the other, Y, can be found by intersecting a circle with radius BX and the segment AC.

In essence, this construction makes use of the fact that XY parallel to AB implies that any guesses Y* (and as a result X*) will also give X*Y* parallel to AB.

In order to construct the equisegment given any A,B, and C, we use a similar idea. Given an angle ABC,

1) Choose a "guess" point Y* the same way as detailed above.

2) Construct the circle C(Y*, AY*) and the line through Y* parallel to BC. Label P the intersection of the circle and line.

3) Construct the circle C(P, PY*) (same as C(P, AY*)) and label C* the intersection of the circle and segment AC.

4) Construct the circle C(C*, PC*) and the line through C* parallel to BC. Label X* the intersection of the circle and line.

5) Construct the line through AX* and label X the intersection of this line and segment BC.

6) Construct the circle C(X, CX) and label Y the intersection of this circle and segment AB.

Then segment XY is the equisegment of triangle ABC.

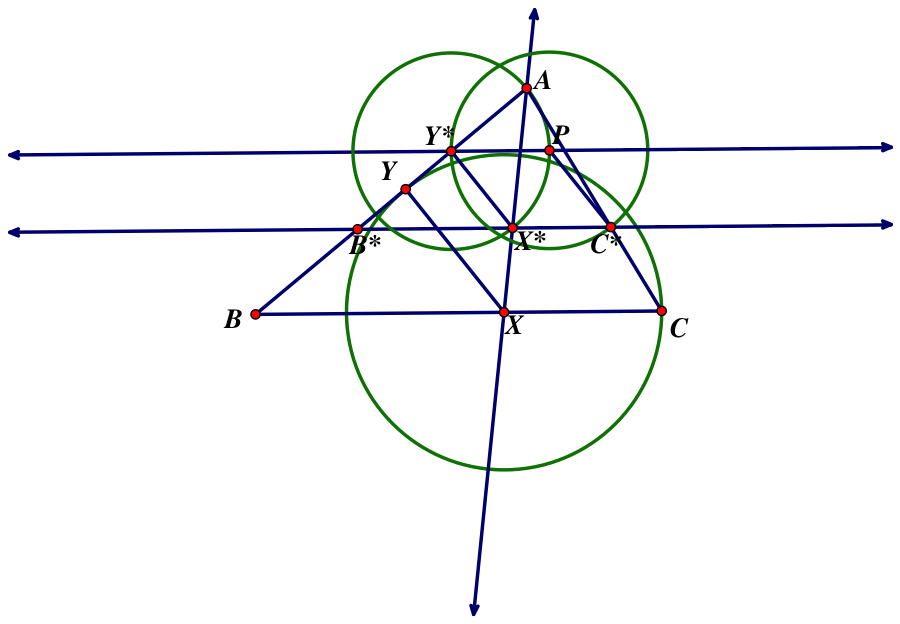
The proof is quite simple. By construction, PC*X*Y* is a rhombus with side length AY*; therefore, AY* = X*Y* = X*C*. Now, also by construction, the line through C* and X* is parallel to segment BC. Hence, triangles AB*C* and ABC are similar by the congruence of all of their angles. We can then consider triangle ABC as a dilation of triangle AB*C* with center of dilation A (since it does not move in the dilation); observe that B* and C* will be dilated onto B and C. Point X is the point corresponding to X* in the dilation, and by similarity, we have the proportionality of corresponding segments; in particular,

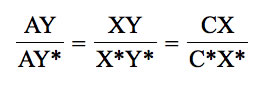
As AY* = X*Y* = X*C* as discussed above, we must have AY = XY = CX. Therefore, segment XY is the equisegment of triangle ABC.