

Orthocenters
by
Bradley Johnson
We will set out to show that the sum of the ratios listed above is 1. To do this we will look at two different expressions for the area of triangle ABC.
Let A be the area of triangle ABC, then we can write our first equation:
(1) 2A = HD*BC + HE*AC + HF*AB.
We can also write the following three expressions for area:
(2) 2A = AD*BC ,
(3) 2A = BE*AC ,
(4) 2A = CF*AB.
We will proceed by taking the sum of (2) , (3) , (4) we get the following expression:
(5) 6A = AD*BC + BE*AC + CF*AB
Now, taking (1) and solving for A, then substituting into (5) we have:
3 [ HD*BC + HE*AC + HF*AB ] = AD*BC + BE*AC + CF*AB
From which we obtain the following:
(6) 3HD*BC = AD*BC
(7) 3HE*AC = BE*AC
(8) 3HF*AB = CF*AB
Equation (6) implies AD/HD = 3
Equation (7) implies BE/HE = 3
Equation (8) implies CF/HF = 3
Our result follows by noticing that the sum we are interested in is the sum of the reciprocals of our previous result. Therefore we have established
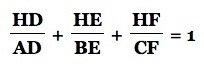
Our next endeavor will be to show the second result from the introduction.
Segments AD, BE, and CF are split into a 2:1 ratio. In the first proof we established which segments were each 1/3 AD, BE, and CF, therefore the segments now in question are the remaining pieces of AD, BE, and CF, thus we find that they are 2/3 of each. and the result follows.