Assignment 1: From a Circle to [Almost] a Square

By Kendyl Wade

First we will graph a few functions:

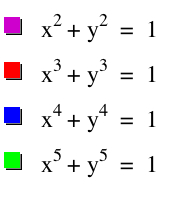
Which resulted in the following graphs:

      Here we can notice that the functions with even exponents resulted in a circular shape with a domain of [-1, 1] and a range of [-1, 1].  Also, the functions with odd exponents resulted in almost a linear function from negative infinity to around x = -1, then resumes that linear function around x = 1.

     One thing to take note of is our first equation, x^2 + y^2 = 1, is the equation of a circle with center (0, 0) and a radius of 1.

Also, if we were to graph the equation with an exponent of 1, we would have x + y = 1, which is just y = -x + 1.

Let's go a little further and look at the function with just even exponents and then just odd exponents:

Even exponents:  

Odd exponents:     

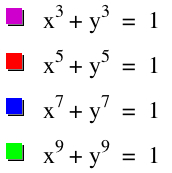
So what can we expect for the graphs of

?

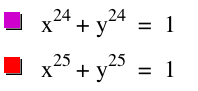
From looking at the previous graphs, the even exponent equations appear to approach the shape of a square and the odd exponents appear to have the line y = -x from negative infinity to -1 and 1 to infinity, then y = 1 from -1 to 1, and x = 1 at 1.

 

So now we see that when our exponent is 24, the function is in the shape of a square with curved corners and side lengths of around 1.

If we were to choose even larger exponents, it should get to look exactly like a square with pointed corners and a piece wise linear function like the line y = -x and the top right half of a square.

Our prediction was correct! But why is that?

 

 

 

 

 

Return