

Assignment 10: Parametric Equations
By Kendyl Wade
For this exploration, we will investigate parametric equations. Specifically, we will look at x = cos(bt) and y = sin(at) for various a and b with
.
Let's look at the case when b=1 and a=1.
It should be no surprise that the graph is of a circle centered at (0, 0) with radius 1.
Now let's see what happens when b=1 and a increases by increments of 1.
It appears that the frequency increases horizontally as a increases, but to get a better feel for this property, let's look at an animation.
It also appears that the value of a represents the number of maximums or minimums on the graph! And all the graphs with even values for a pass through the origin.
Now let's see what happens when a=1 and b increases by increments of 1...
Now it appears that as b increases, the frequency increases vertically.
While playing on Graphing Calculator, I noticed something interesting. Let's see what happens when b = a/2...
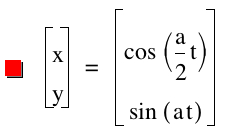
Here is a video that shows the graph with 1 < a < 100.
As you can see, the graph maintains the same general shape, but the frequency increases.